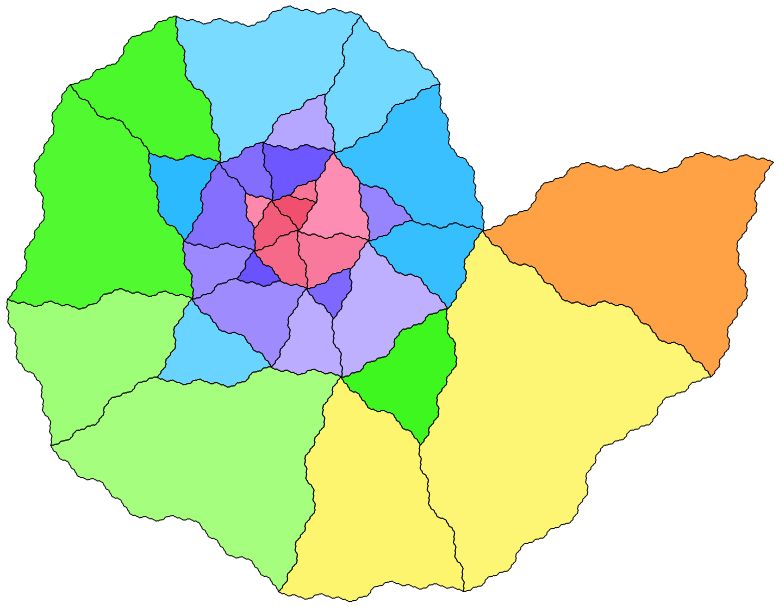
Here is code for the cow-nautilus. It could probably be simplified.
r=Root[-1-#1^2+#1^3&,3]; s=Root[-1-#1^2+#1^3&,1]; add= RootReduce[{2-s,2s-s^3,-s+s^2}]; iterate=5;
cowed[comp_]:= First/@Split[Flatten[RootReduce[#[[1]]+(#[[2]]-#[[1]]){0,-r^5,r^5+1,1}]&/@Partition[comp,2,1,1],1]];
vecs={{{4,3,6},{0,0,0},{-6,-4,-9},{7,5,10},{0,0,0},{-1,-1,-2},{-3,-2,-5},{1,1,1},{0,0,0},{2,1,3},{5,3,7},{-1,-1,-2},{0,0,0},{-3,-2,-4},{-7,-5,-10},{2,1,3},{0,0,0},{4,3,6},{10,7,15},{-3,-2,-4}},{{-1,0,-1},{2,2,3},{4,3,6},{-5,-3,-7},{4,3,6},{2,2,3},{1,1,1},{7,5,10},{-5,-3,-7},{4,3,6},{10,7,15},{-18,-12,-26}}};
naut=RootReduce[Join[Partition[{1,r,r^2}.#&/@vecs[[1]],4],Flatten[Table[Partition[({1,r,r^2}.#&/@vecs[[2]]),4](-r)^n,{n,-8,0}],1]]];
poly=ReIm[Nest[cowed[#]&,#,iterate]]&/@N[naut,50];
Graphics[{EdgeForm[{Black}],MapIndexed[{ColorData["BrightBands"][N[Norm[Mean[#1]]/2]],Polygon[#1]}&,poly]}, ImageSize-> 600]
Here's alternate code all in terms of the root, which I've also placed in the initial post.
r=Root[-1-#1^2+#1^3&,3]; iterate=6;
cowed[comp_]:= First/@Split[Flatten[RootReduce[#[[1]]+(#[[2]]-#[[1]]){0,-r^5,r^5+1,1}]&/@Partition[comp,2,1,1],1]];
base={{r^10,r^7,-r^9,r^11},{-r^12,-r^9,r^11,-r^13},{r^8,r^5,-r^7,r^9},{-r^7,-r^4,r^6,-r^8}}+{-r^10,r^11,-r^6,r^4+r^8};
naut=RootReduce[Join[Table[base[[1]] (-r)^n,{n,0,-4,-1}],Flatten[Table[Drop[base,1](-r)^n,{n,-8,0}],1]]];
poly=ReIm[Nest[cowed[#]&,#,iterate]]&/@N[naut,50];
Graphics[{EdgeForm[{Black}],MapIndexed[{ColorData["BrightBands"][N[Norm[Mean[#1]]/2]],Polygon[#1]}&,poly]},ImageSize-> 800]
It looks slightly different since I shifted one of the triangles.