I have a rather basic problem where I am asked to create a network of 300 nodes that can be clustered into 100-node chunks. Essentially, the nodes have many connections within a chunk and comparatively few between different100-node chunks.
For example, if I made the connections with a chunk occur with 100% probability and between chunks occur 0% I get the following:
edges = {};
For[l = 1, l <= 3 , l++, h = 100*l;
For[n = 100 (l - 1) + 1, n < 100*l + 1, n++,
For[m = n + 1, m <= 300, m++,
If[m <= h,
If[RandomReal[{0, 1}] > 0.0, AppendTo[edges, n <-> m]],
If[RandomReal[{0, 1}] > 0.99, AppendTo[edges, n <-> m]]]]]]

which is expected and gives a corresponding MatrixPlot of the Adjacency Matrix as:
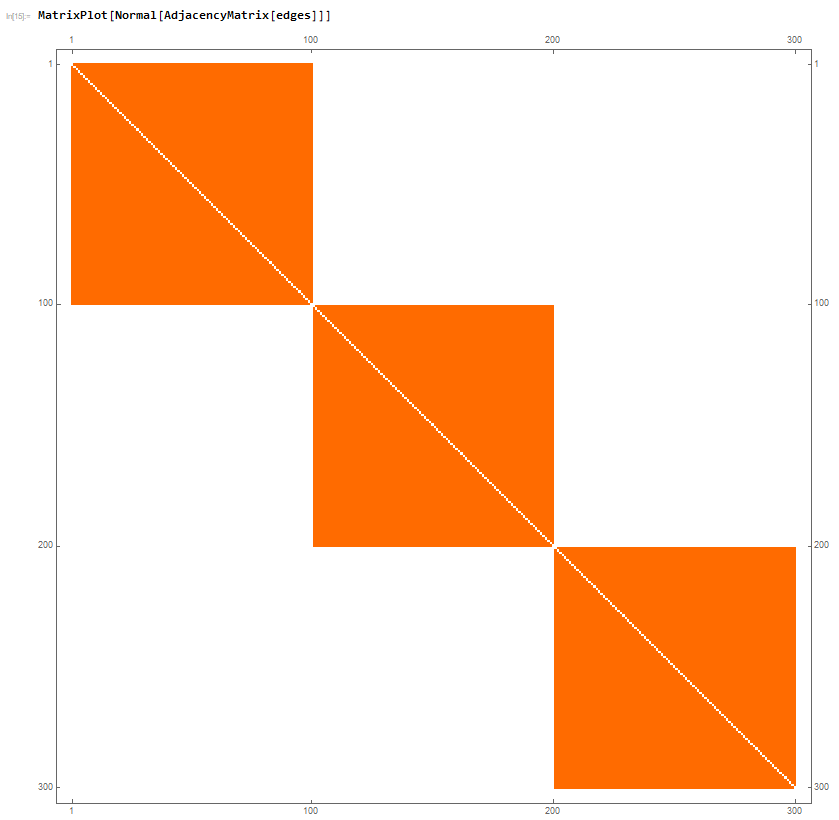
Which is also all well and good. Now, something very strange seems to be going on when I try to make the connections between the 100-node chunks be non zero. For example, if I made the probability be 1%, the folowing is obtained:

This looks ok, but it becomes very evident that there is a problem when one looks at the corresponding Matrix Plot of the Adjacency Matrix 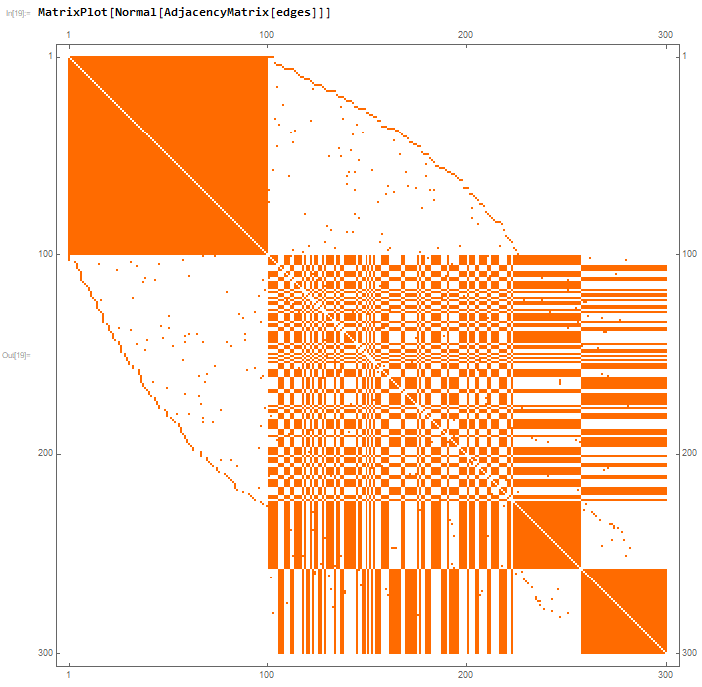
Evidently, there is a very big problem somewhere. I did try to check this in a bit more detail and it seems that everything is working properly with the Matrix Plot. It seems that there is somewhere a problem with my code - but where? The code, in my opinion, seems rather simple and straightforward. I am really confused with what the issue is and could use assistance, it doesn't seem possible that Mathematica would have a problem with something so basic.