Hello,
heqn = D[u[x, t], t] == c*D[u[x, t], {x, 2}] - A*u[x, t] - B;
ic = u[x, 0] == 2*A/b;
bc = {u[0, t] == 0, u[500, t] == 0};
sol = DSolve[{heqn, ic, bc}, u[x, t], {x, t}]
(* returns unevaluated *)
If a symbolic solver returns unevaluated, then Mathematica can't solve the problem.
DSolve[]'s symbolic support for PDE's is still somewhat limited, so don't be surprised if some things don't work yet.
Numeric solution:
NDSolve[] needs numeric values for constans.
A = 1;
B = 2;
c = 1/10;
b = 3;
heqn = D[u[x, t], t] == c*D[u[x, t], {x, 2}] - A*u[x, t] - B;
ic = u[x, 0] == 2*A/b;
bc = {u[0, t] == 0, u[500, t] == 0};
sol = NDSolve[{heqn, ic, bc}, u, {x, 0, 1}, {t, 0, 1}]
Plot3D[u[x, t] /. sol, {x, 0, 1}, {t, 0, 1}, AxesLabel -> Automatic]
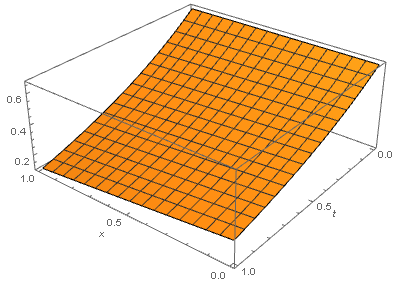
Comparison with Maple 2017.3 symbolic pdsolve solver:
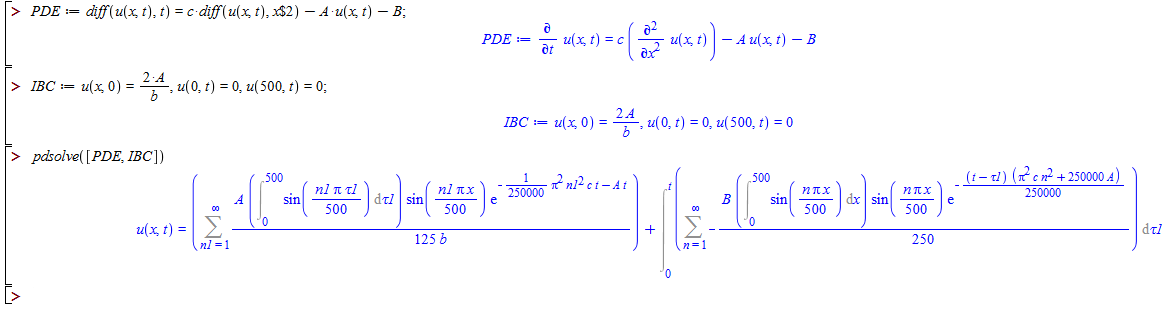
Regards,Mariusz.