For my research project I had to encounter a thorny problem. But before I tell about the problem I would like to briefly mention something about my research project. Basically I am using embryonic stem cells that self-organize to form spheroids (balls of cells) to study gastrulation events. In order to not bog down the readers with technical jargon, gastrulation is a process where the stem cells start to form the different layers; each layer then goes onto form the various tissues/organs, in the process unraveling the developmental plan of the entire organism. I am using experimental techniques and quantitative principles from biophysics and engineering to understand some aspects of this crucial process
Now coming back to the problem at hand, the gastruloids (image below) are quite rough in their appearance and not as beautiful as one would like them to be (only a mother can love such an image). Any means of quantifying these gastruloids requires me to initially segment them. When you see a time-lapse images of gastruloids it becomes apparent that they shed a lot of cells (for reasons I do not know yet). This adds considerable noise to the system; oftentimes to the point that as a human my eyes are fooled and run into the difficulty of finding the right contours for the spheroids. Here comes the disclosure: classical means/operations in image-processing (gradients and edge detection, filtering, morphological operations etc.. ) prove utterly futile for image segmentation in my case.
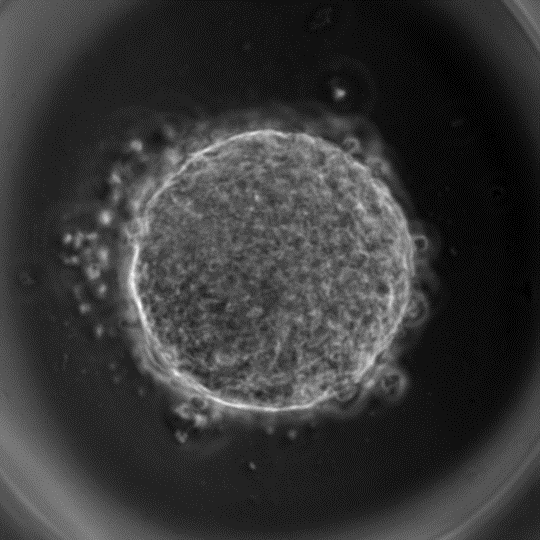
(A gastruloid virtually a ball of cells with many shed around the periphery)
So what can you do to address the problem where even the best image processing tool in existence the human eyes fails. This is precisely where you take help of neural networks. Neural networks are selling like hotcakes during the recent years and added life and hope to the once dead area of artificial intelligence. Again to avoid underlying technical details, neural networks is a paradigm utilized by the computer to mimic the working of a human brain by taking into account the complex interactions between the cells but only digitally. There are many flavours of neural networks out there, each one geared towards performing a specific task. With advancements made in the area of deep learning/artificial intelligence, the neural nets have started to surpass humans in tasks that humans have been known to be best for i.e. classification tasks. A few recent examples that come to mind include Googles AlphaGo beating the former World Go champion and an AI diagnosing skin cancer with an unprecedented accuracy.
I utilized one such flavour of neural networks (a deep convolutional network termed as UNET) to solve my longstanding problem. I constructed the network in Wolfram-Language with external help from Alexey Golyshev. UNET is a deep convolutional network that has a series of convolutional and pooling operations in the contraction phase of the net (wherein the features are extracted) and a sequence of deconvolution & convolution operations in the expansion phase which then yields an output from the network. This output can be subjected to a threshold to ultimately generate a binarized mask (the image segmentation).
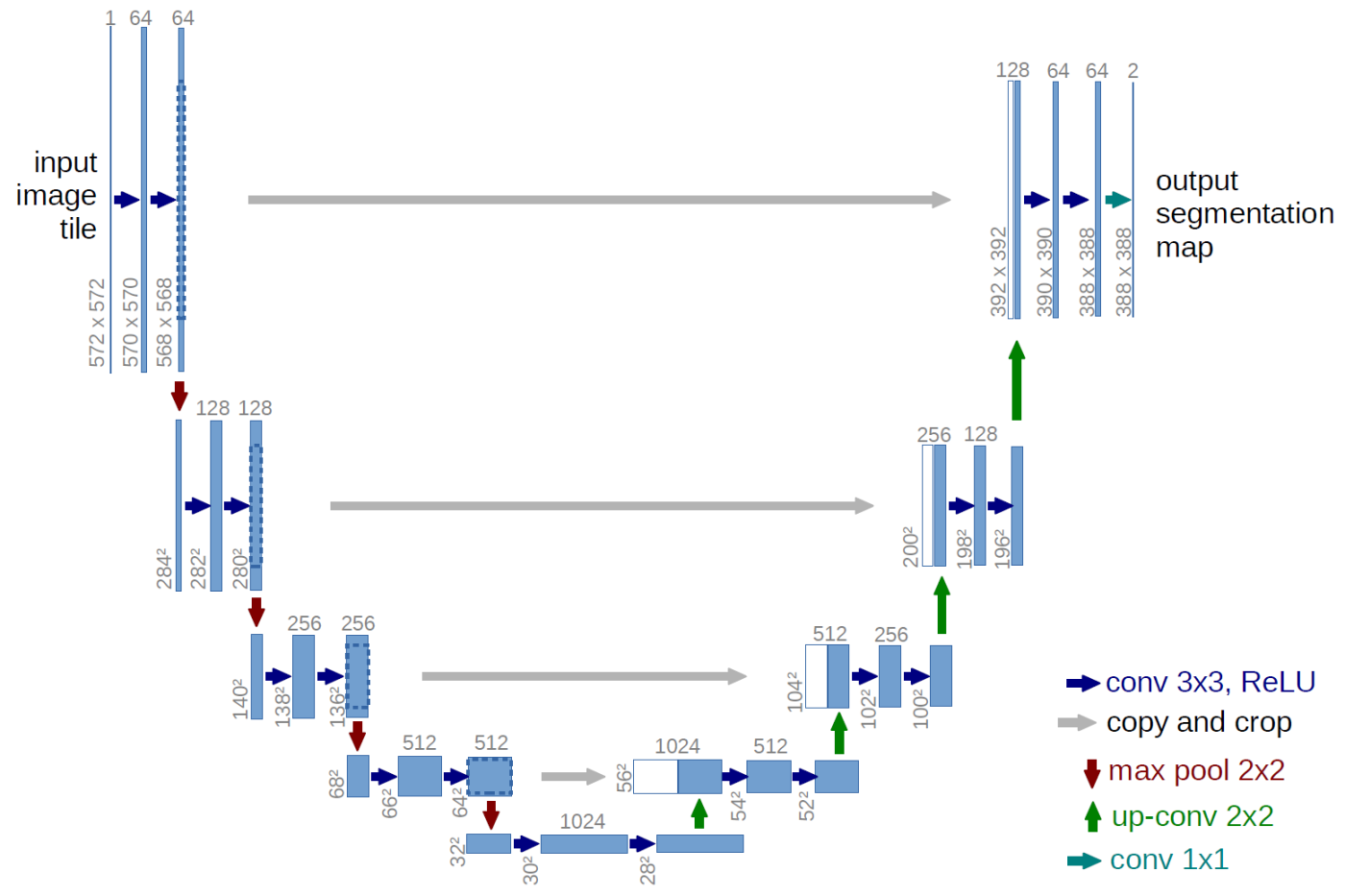
The architecture of UNET as provided by the author: https://lmb.informatik.uni-freiburg.de/people/ronneber/u-net/
(* ::Package:: *)
BeginPackage["UNETSegmentation`"]
(* ::Section:: *)
(*Creating UNet*)
conv[n_]:=NetChain[
{
ConvolutionLayer[n,3,"PaddingSize"->{1,1}],
Ramp,
BatchNormalizationLayer[],
ConvolutionLayer[n,3,"PaddingSize"->{1,1}],
Ramp,
BatchNormalizationLayer[]
}
];
pool := PoolingLayer[{2,2},2];
dec[n_]:=NetGraph[
{
"deconv" -> DeconvolutionLayer[n,{2,2},"Stride"->{2,2}],
"cat" -> CatenateLayer[],
"conv" -> conv[n]
},
{
NetPort["Input1"]->"cat",
NetPort["Input2"]->"deconv"->"cat"->"conv"
}
];
nodeGraphMXNET[net_,opt: ("MXNetNodeGraph"|"MXNetNodeGraphPlot")]:= net~NetInformation~opt;
UNET := NetGraph[
<|
"enc_1"-> conv[64],
"enc_2"-> {pool,conv[128]},
"enc_3"-> {pool,conv[256]},
"enc_4"-> {pool,conv[512]},
"enc_5"-> {pool,conv[1024]},
"dec_1"-> dec[512],
"dec_2"-> dec[256],
"dec_3"-> dec[128],
"dec_4"-> dec[64],
"map"->{ConvolutionLayer[1,{1,1}],LogisticSigmoid}
|>,
{
NetPort["Input"]->"enc_1"->"enc_2"->"enc_3"->"enc_4"->"enc_5",
{"enc_4","enc_5"}->"dec_1",
{"enc_3","dec_1"}->"dec_2",
{"enc_2","dec_2"}->"dec_3",
{"enc_1","dec_3"}->"dec_4",
"dec_4"->"map"},
"Input"->NetEncoder[{"Image",{160,160},ColorSpace->"Grayscale"}]
]
(* ::Section:: *)
(*DataPrep*)
dataPrep[dirImage_,dirMask_]:=Module[{X, masks,imgfilenames, maskfilenames,ordering, fNames,func},
func[dir_] := (SetDirectory[dir];
fNames = FileNames[];
ordering = Flatten@StringCases[fNames,x_~~p:DigitCharacter.. :> ToExpression@p];
Part[fNames,Ordering@ordering]);
imgfilenames = func@dirImage;
X = ImageResize[Import[dirImage<>"\\"<>#],{160,160}]&/@imgfilenames;
maskfilenames = func@dirMask;
masks = Import[dirMask<>"\\"<>#]&/@maskfilenames;
{X, NetEncoder[{"Image",{160,160},ColorSpace->"Grayscale"}]/@masks}
]
(* ::Section:: *)
(*Training UNet*)
trainNetwithValidation[net_,dataset_,labeldataset_,validationset_,labelvalidationset_, batchsize_: 8, maxtrainRounds_: 100]:=Module[{},
SetDirectory[NotebookDirectory[]];
NetTrain[net, dataset->labeldataset,All, ValidationSet -> Thread[validationset-> labelvalidationset],
BatchSize->batchsize,MaxTrainingRounds->maxtrainRounds, TargetDevice->"GPU",
TrainingProgressCheckpointing->{"Directory","results","Interval"->Quantity[5,"Rounds"]}]
];
trainNet[net_,dataset_,labeldataset_, batchsize_:8, maxtrainRounds_: 10]:=Module[{},
SetDirectory[NotebookDirectory[]];
NetTrain[net, dataset->labeldataset,All,BatchSize->batchsize,MaxTrainingRounds->maxtrainRounds, TargetDevice->"GPU",
TrainingProgressCheckpointing->{"Directory","results","Interval"-> Quantity[5,"Rounds"]}]
];
(* ::Section:: *)
(*Measure Accuracy*)
measureModelAccuracy[net_,data_,groundTruth_]:= Module[{acc},
acc =Table[{i, 1.0 - HammingDistance[N@Round@Flatten@net[data[[i]],TargetDevice->"GPU"],
Flatten@groundTruth[[i]]]/(160*160)},{i,Length@data}
];
{Mean@Part[acc,All,2],TableForm@acc}
];
(* ::Section:: *)
(*Miscellaneous*)
saveNeuralNet[net_]:= Module[{dir = NotebookDirectory[]},
Export[dir<>"unet.wlnet",net]]/; Head[net]=== NetGraph;
saveInputs[data_,labels_,opt:("data"|"validation")]:=Module[{},
SetDirectory[NotebookDirectory[]];
Switch[opt,"data",
Export["X.mx",data];Export["Y.mx",labels],
"validation",
Export["Xval.mx",data];Export["Yval.mx",labels]
]
]
EndPackage[];
The above code can also be found in the repository @ Wolfram-MXNET GITHUB
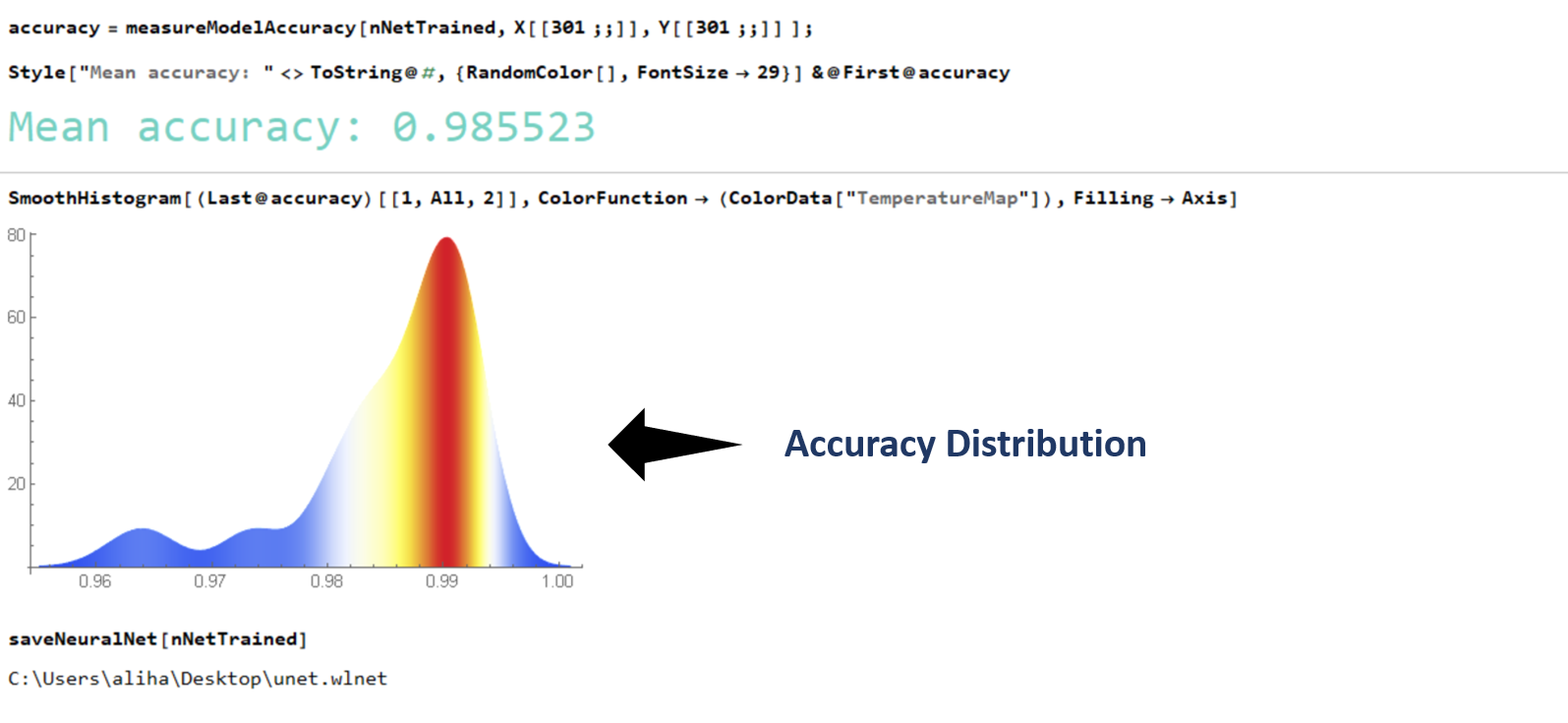
I trained my network over my laptop GPU (Nvidia GTX 1050) by feeding an augmented data (a set of 300 images constructed from a small dataset) . The training was done in under 3 minutes !. The accuracy (computed as the Hamming Distance between two vectors) of the generated binary masks with respect to the ground truth (unseen data) for a set of 90 images was 98.55 %. And with this a task that previously required me to painstakingly trace the contour of the gastruloids manually can now be performed in a matter of milliseconds. All the saved time and perspiration to be utilized somewhere else?
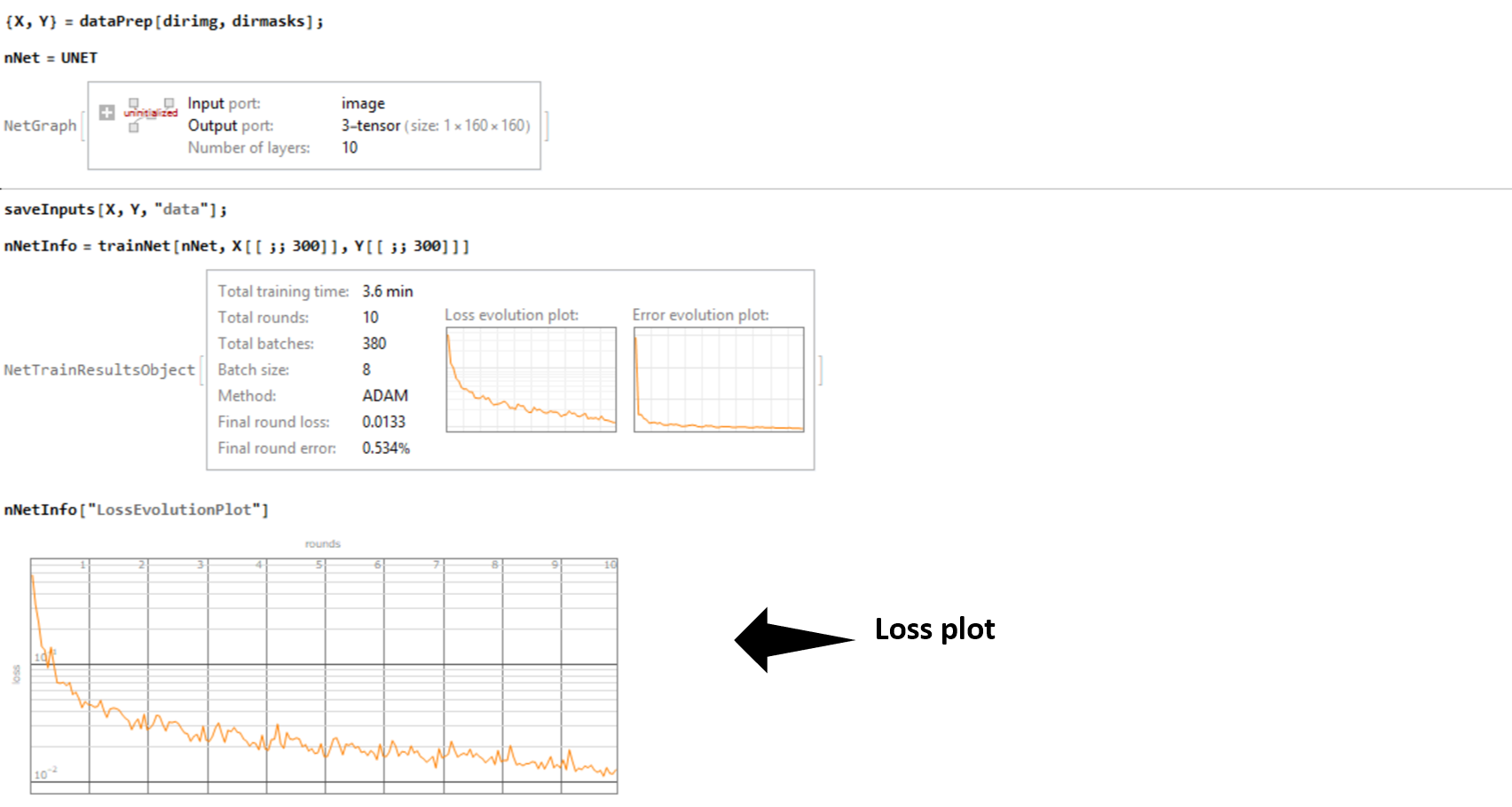
Below is the results obtained by applying our trained net on one input:
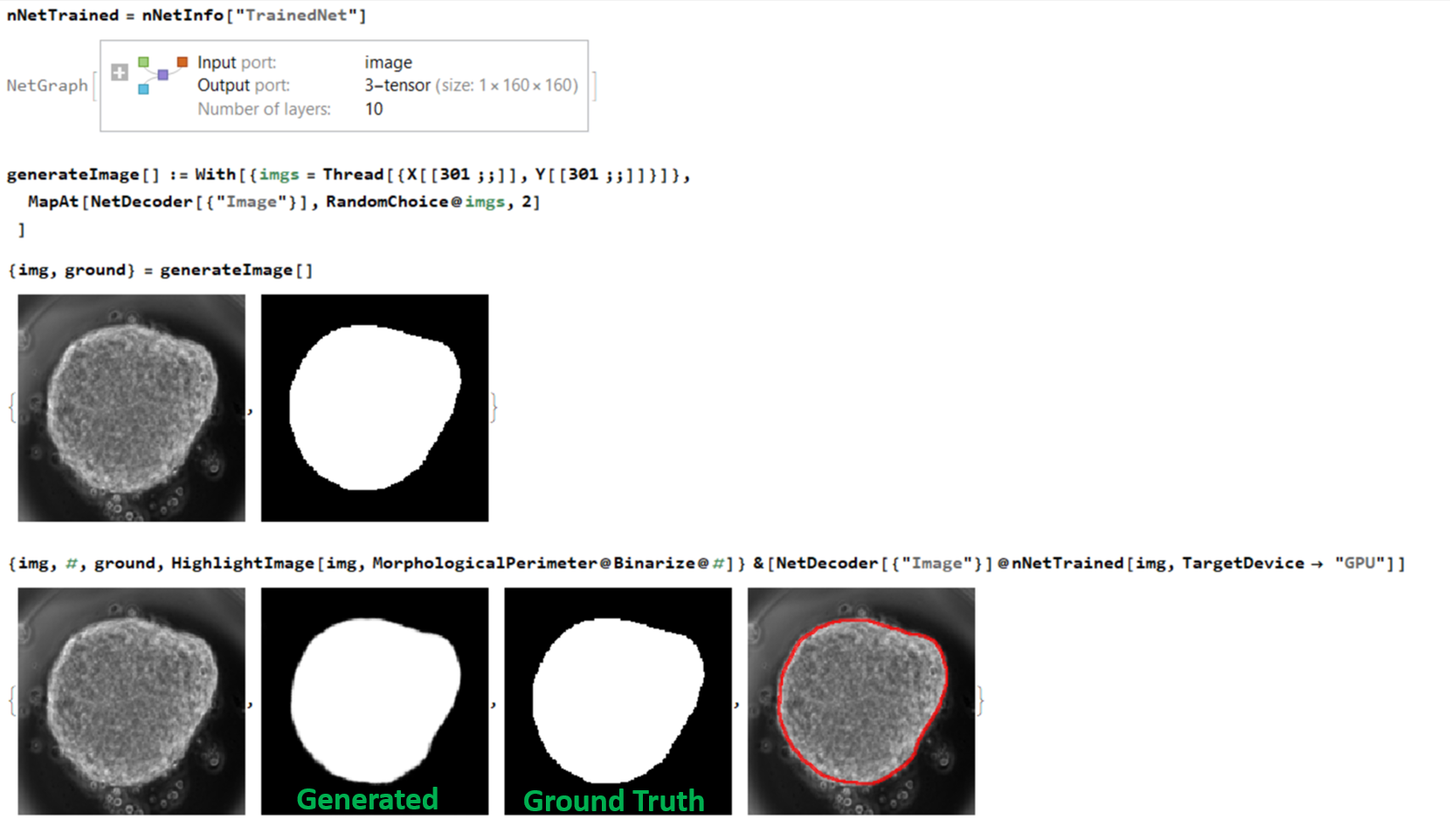
The interesting aspect for me regarding the network was that despite my gastruloids being highly dynamic (changing shape over time) I never had to explicity state it to the network. All the necessary features were learned from the limited number of images that I trained my network with. This is the beauty of the neural network.
Finally the output of the net as applied on a number of unseen images:

Note: I have a python MXNET version of UNET @ python mxnet GITHUB
The wolfram version of UNET however seems to outperform the python version even though it also utilizes MXNET at the back-end for implementing neural networks. It should not come as a surprise because my guess is that the people at Wolfram Research may have done internal optimizations on top of the library