I have some code that outputs what I want, although I may change the function later. However, I want the output to be like a screenshot I have provided, such that it fades as with the properties of another function.
Here is the code:
ClearAll["Global`*"]; xi = 2; k0 = 9; Print["k0=", k0, " xi=", xi]; \
Show[Table[
sol = NDSolve[{D[xtraj[t],
t] == (Sinh[
xtraj[t] (t - xi)])/((Cos[xtraj[t]]) + (Cosh[
xtraj[t] (t - xi)])), xtraj[0] == n}, xtraj[t], {t, 0, 4}];
ParametricPlot[{t, xtraj[t]} /. sol, {t, 0, 4}, PlotRange -> All,
PlotStyle -> {Blue, Full, Medium}, AxesStyle -> Thickness[.003],
LabelStyle -> {Black, Medium}, AxesLabel -> {xtraj, t}], {n, -4,
4 - 0.5, 0.5}]]
Here is the output - or a simplified version of it:
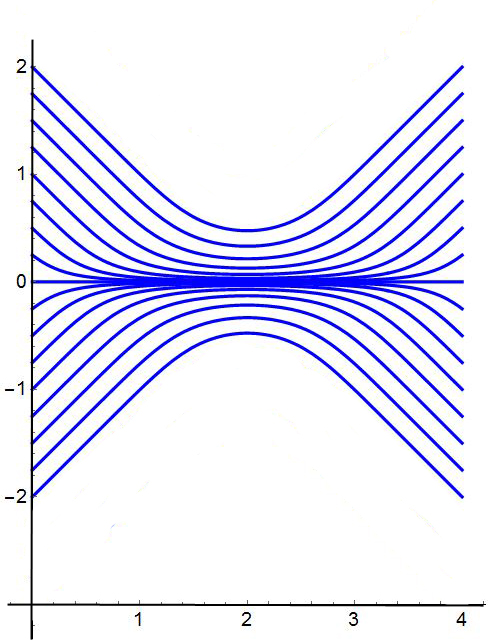
And now this is what I would like - the fading is based upon another function - given below. 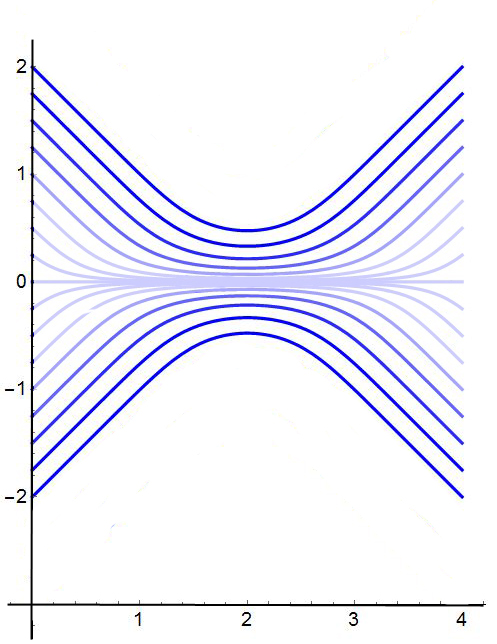
Here is the fading function:
(E^(-2 (-2 + t + x)^2) Sqrt[2 \[Pi]] (1 + E^(8 (-2 + t) x) + 2 E^(4 (-2 + t) x) Cos[10 x]))
It is a tricky one that I really would like to solve.