@Jon,
These boundary conditions do not like each other:
temp[5, 0] == 301
temp[5, t] == 47
Even the evolvement of the temperature is not known, it is required to define such process instead of using arbitary abrupt change here.
Here is a modification of your system: (Coefficients are adjusted for better visualization):
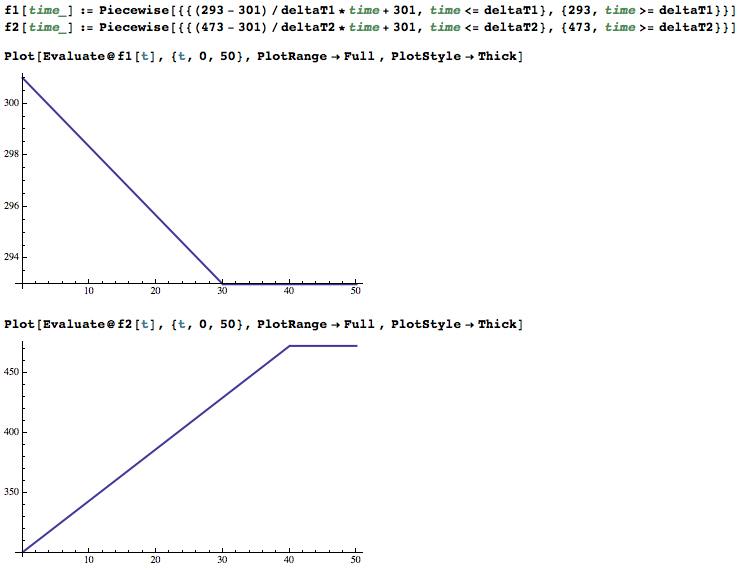
lets assume that we know the time used for heating up and cooling down both ends. You can adjust them later
deltaT1 = 30;
deltaT2 = 40;
Then I use the piecewise function here to approximate thermal exchange processes at two ends with first order:
f1[time_] := Piecewise[{{(293 - 301)/deltaT1*time + 301, time <= deltaT1}, {293, time >= deltaT1}}]
f2[time_] := Piecewise[{{(473 - 301)/deltaT2*time + 301, time <= deltaT2}, {473, time >= deltaT2}}]
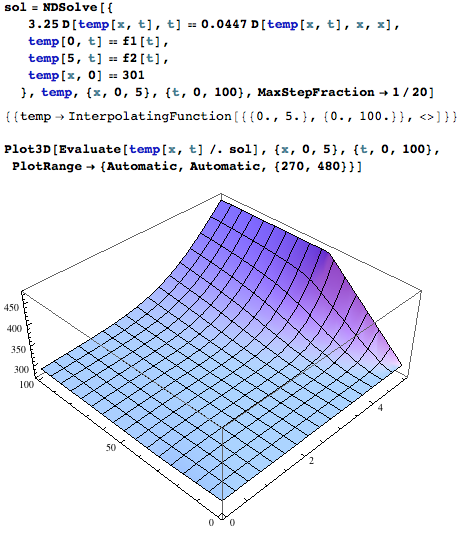
Once I have these steps specified, I can find how the 1-d rod respond to the time-dependent temperature profile at its two ends:
sol = NDSolve[{
3.25 D[temp[x, t], t] == 0.0447 D[temp[x, t], x, x],
temp[0, t] == f1[t],
temp[5, t] == f2[t],
temp[x, 0] == 301
}, temp, {x, 0, 5}, {t, 0, 100}, MaxStepFraction -> 1/20]
Plot3D[Evaluate[temp[x, t] /. sol], {x, 0, 5}, {t, 0, 100},
PlotRange -> {Automatic, Automatic, {270, 480}}]
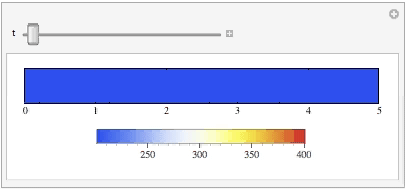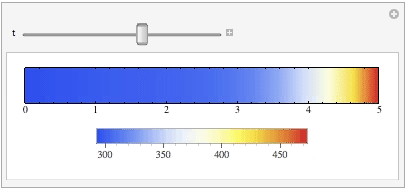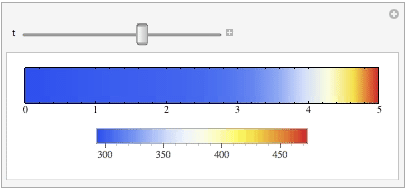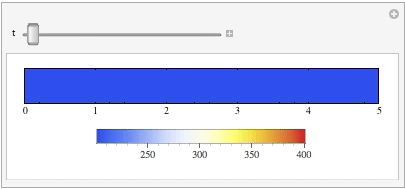
With Manipulate function, I can visualize the evolvement of the thermal system over 100 time steps
Manipulate[
DensityPlot[
Evaluate[temp[x, t] /. sol], {x, 0, 5}, {y, -0.02, 0.02},
ColorFunction -> (ColorData["TemperatureMap"][#1] &),
PlotRange -> {{0, 5}, {-0.01, 0.01}, {270, 480}},
PlotLegends -> Automatic, AspectRatio -> 0.1, MaxRecursion -> 3,
FrameTicks -> {Automatic, None}],
{t, 0, 100}]