Divide a cuboid into two cuboids similar to the original shape. The answer involves the cube root of 2, otherwise known as the Delian constant. I've called this object the Delian Brick. It's a 3D 2-reptile. A stack of three bricks can be made using the cube root of 3, and so on.
With[{r=2^(1/3)},
Graphics3D[{Opacity[.5],
Cuboid[{0 r^0,0 r^1,0r^2},{1 r^0,1r^1,1r^2}], Cuboid[{1 r^0,0 r^1,0r^2},{2 r^0,1 r^1,1r^2}]},SphericalRegion-> True, Boxed-> False]]
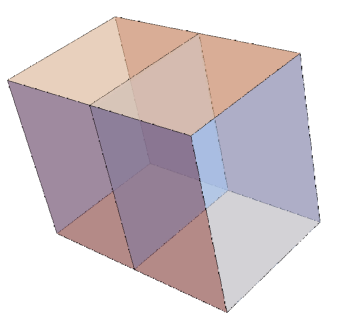
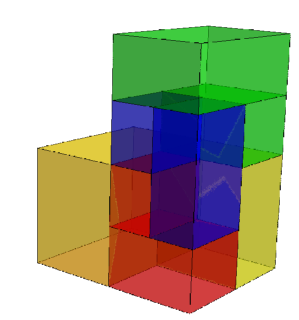
I'd self-discovered the Delian Brick myself, as did at least ten other recreational mathematicians I've exchanged correspondence with. It may have been known to the ancient greeks. The first publication I've found is by Dale Walton and the game company Thinkfun, who expanded it into a 3D 4-irreptile they called the Fifth Chair puzzle.
With[{r=2^(1/3)},
Graphics3D[{Opacity[.5],
{Red,Cuboid[{0 r^0,0 r^1,0r^2},{2 r^0,r^1,r^2}], Cuboid[{1 r^0,1 r^1,0r^2},{2 r^0,2 r^1,1r^2}]},
{Blue,Cuboid[{0 r^0,1 r^1,0r^2},{1 r^0,3r^1,1r^2}], Cuboid[{1 r^0,2 r^1,0r^2},{2 r^0,3 r^1,1r^2}]},
{Green,Cuboid[{0 r^0,3 r^1,0r^2},{2 r^0,4r^1,2r^2}], Cuboid[{0 r^0,2 r^1,1r^2},{2 r^0,3 r^1,2r^2}]},
{Yellow, Cuboid[{2 r^0,0 r^1,0r^2},{4 r^0,2r^1,2r^2}], Cuboid[{0 r^0,0 r^1,1r^2},{2 r^0,2 r^1,2r^2}]}}, SphericalRegion-> True, Boxed-> False]]
There are also five space-filling tetrahedra, and at least two of them are 8-reptiles
Row[{Graphics3D[{Opacity[.5],Polygon/@Union[Sort/@
Flatten[Subsets[#,{3}]&/@(IntegerDigits/@({{020,111,121,022},{022,111,112,222},{022,111,121,222},{022,113,112,222},{022,113,123,024},{022,113,123,222},{111,202,212,113},{111,222,212,113}}+111)-1),1]]}, Boxed-> False, SphericalRegion->True],
Graphics3D[{Opacity[.5],Polygon/@Union[Sort/@
Flatten[Subsets[#,{3}]&/@(IntegerDigits/@({{002,022,111,113},{022,042,131,133},{022,222,111,113},{022,222,111,131},{022,222,113,133},{022,222,131,133},{111,131,220,222},{113,133,222,224}}+111)),1]]}, Boxed-> False, SphericalRegion->True]}]
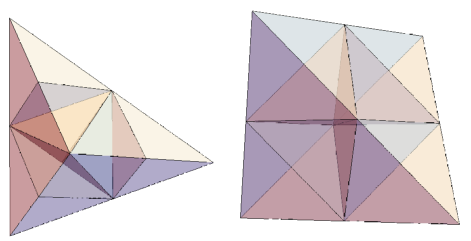
More of these self-similar 3D dissections are listed at 3D Rep-Tiles and Irreptiles. The ones I list here need to be added there. Most of the 3D rep-tiles are based on either a 2D reptile or a polycube. The four items in this discussion fit in neither of those categories. Are there others?
 Attachments:
Attachments: