Empirically derived conditional distribution of System symbols

Range->Length->Part is commonly found in:

Given that Mathematica is a symbolic language it would be interesting to view the relationships between these symbols e.g. Length[List[1,2,3]] implies a relationship of Length -> List.

Since we do not know this information, we will have to retrieve it. For that, I headed to GitHub. Note: GitHub's public api limits the rate you can query to $1$ query every $30$ seconds (so the crawl takes many hours).

(* Get repositories marked with Mathematica as a language *)
githubResults = SearchRepositories["Mathematica"];

"8586 public repositories with language(s): Mathematica.
Only the first 1000 are available via the public api."


(* Get repository names *)
repositoriesWithMathematica = Normal[githubResults[All, "full_name"]];

(* Search for .nb files in these repos *)
notebookResults = SearchNotebooks[repositoriesWithMathematica];
"3525 notebooks found."


(* Now go download all of those .nbs *)
files = DownloadRawURLs[notebookResults, CreateDirectory[]]

With our $3,525$ notebooks, we are ready to try and extract the Symbol->Symbol relationship (thanks to Carl Woll for helping with this part):

Test for system symbol

SetAttributes[systemSymbol, {Listable, HoldFirst}]

systemSymbol[Symbol[_String]] = False;
systemSymbol[s_Symbol] := Context[s] === "System`"
systemSymbol[_] = False;

Extract symbol relationships

Note, we replace all non system symbols with a placeholder "NonWolfram".

NBExpressionRelations[file_] := Module[
  {
   nb = NotebookImport[file, "Input"],
   expr =
    Cases[nb,
     p : _Symbol?systemSymbol[s_Symbol, ___] :> Hold[p], {3, Infinity}]
   },
  Cases[nb,
   p_Symbol?systemSymbol[s_Symbol[___], ___] :>
    If[Context[s] === "System`", RuleDelayed[p, s],
     RuleDelayed[p, "NonWolfram"]], {3, Infinity}]
  ]

Just loop this over all the files to get the data, and then

(* if you want to keep them by file *)
results = AssociationThread[fileNames, expressionData]
(* or *)
data = Flatten[expressionData]

Explore System symbol relationships

(* Tally over the keys (symbols used as Heaed) *)
tally = Tally[data[[;; , 1]]];

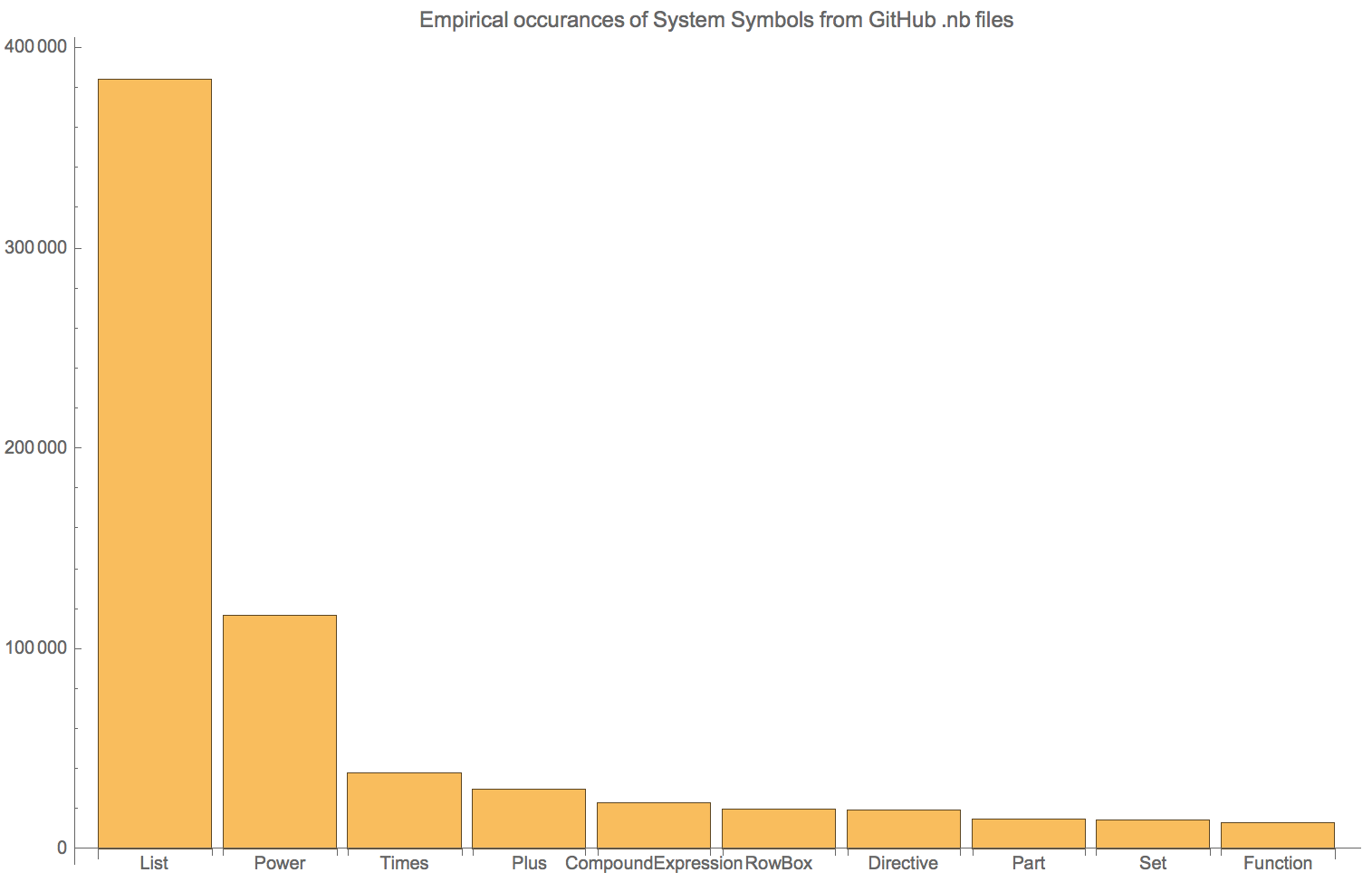
If we just look at the symbols by occurrence, we see that unsurprisingly List is the most prominent:

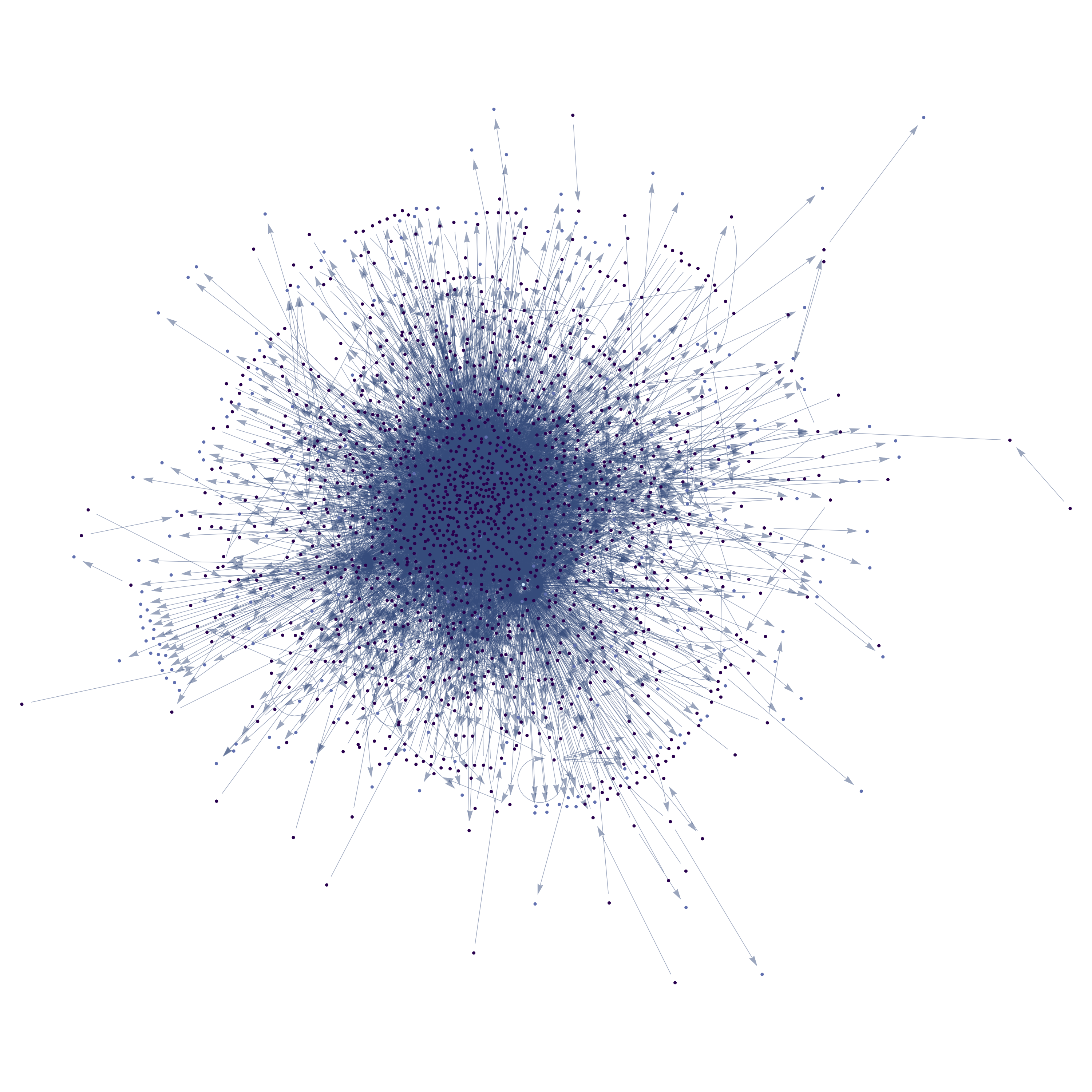
We can view the interaction network as well, where the vertices are colored and sized by occurrence.

ToString[#[[1]]] \[DirectedEdge] ToString[#[[2]]] & /@ data;

The light blue dot near the center is List.

This isn't all that informative, but we can make the frequency distribution of the symbols

NormalizeAssociation[assoc_] :=
 With[{tots = Total[assoc]}, Reverse[Sort[Map[N[#/tots] &, assoc]]]]
(* Occurances of symbols *)
symOccur = Association @@ Rule @@@ tally;
(* Probability of symbols *)
symProb = NormalizeAssociation[symOccur];

and then the conditioned distribution

(* Conditional occurances of symbols *)

symCondOccur =
  Map[Association @@ Rule @@@ Tally[#[[;; , 2]]] &,
   GroupBy[Rule @@@ data, First]];
(* Conditional probability of symbols *)

symCondProb = Map[NormalizeAssociation, symCondOccur];

with this we can traverse our network (in this case we take only the most likely at each step, which may not be the best approach overall)

nextSymbol[symbol_] := Module[
  {

   dist, max, sel, key
   },
  If[symbol == Nothing, Return[Nothing]];

  dist = symCondProb[symbol];

  (* Maybe we never saw this symbol as head in our data *)

  If[MissingQ@dist, Return[Nothing]];
  max = Max[symCondProb[symbol]];
  sel = Select[dist, max == # &];

  (* Likewise perhaps selection failed as it was not connected to anything *)
  If[sel == <||>, Return[Nothing]];
  key = First@Keys[sel];

  (* Since we always take max,
  if key\[Equal]symbol we will go in circles *)

  If[key == symbol, Return[Nothing]];
  Return[key];
]
  ```


Now we can see some promising results:

NestList[nextSymbol[#] &, Range, 5] `` yields:{Range, Length, Part}`

NestList[nextSymbol[#] &, Import, 4]

yields: {Import, StringJoin, NotebookDirectory, EvaluationNotebook}

so it seems people tend to write Range[Length[Part[...]]] e.g. Range@Length@myData[[;;,1]] and Import[StringJoin[NotebookDirectory[],...]]

Whats next?

Next it would be interesting to throw these notebooks into a language model.

Code

Attached is the code for crawling, everything else of relevance is above.

Attachments:

GitHub.m