Numerical Cognition in Wolfram Alpha

One of the result features of single digit addition on Wolfram Alpha includes the time it will take humans of different ages to carry the specified computation.

WolframAlpha["1+1", {{"TypicalHumanComputationTimes", 1},"FormattedData"}]

age 6: 3.2 seconds, age 8:1.8 seconds, age 10: 1.2 seconds, age 18: 0.83 seconds

These data are calculated from algorithms found in a series of cognitive science experiments which aimed at categorizing the reaction time of human numerical computation abilities.This was the inception of the question of how to use the Wolfram language to further query human numerical abilities. This seems particularly useful for studying higher level mathematical abilities in algebra and calculus. It is possible to imagine the use of reaction times across a wide range of problems in order to identify deviations that might indicate misunderstanding or areas of weakness.

There is a lot that can be learned from reaction time data from simple numerical cognition trials. Furthermore, deploying a numerical cognition experiment to the web could include not only more participants than a lab experiment, but it could also include a broader population. For example, it would be possible to compare reaction time variation across participants of different ages, different math skill levels, and different counties.

The project in a nutshell

In this project, we aimed at deploying cognitive experiment trials online. We hoped to used the Wolfram language's flexible design to both run a dynamic experiment online and to collect/analyze behavioral data.

The Wolfram language has full functionality to deploy a notebook-programmed cognitive experiment to the web and to collect behavioral data. We were able to web deploy a fraction magnitude estimation task and to collect reaction time data through Wolfram Data Drop capabilities. These data were subsequently accessed and analyzed within a Wolfram language notebook.

The Layout

The simple task we wanted to develop was a fraction numerical magnitude estimation judgement. Participants would be presented with a fraction ranging in value from 0 to 1 and had to judge whether the numerical value was closer to one or zero by pressing the "0" or "1" buttons on the left and right bottom of the screen (see picture above).

The general approach was to create a dynamic module which could switch from one overlay to another given an action. In this case, each overlay was the presentation of a stimuli and the action was the press of a response button.

Grids were used as the overlay to be able to control most aspects of the stimuli screen. This included the relative position of the stimuli and their size.

The skeleton of the program is presented below.

DynamicModule[
 {},
 Dynamic[
  Overlay[{
    Grid[{}],
    Which[TrueQ[], Grid[{}], TrueQ[], Grid[{}]],
    Which[TrueQ[], Grid[{}], TrueQ[], Grid[{}]],
    Grid[{},
     {Which[TrueQ[pressed == 1], 1, TrueQ[pressed == 2],
       2, TrueQ[pressed == 3], 3, TrueQ[pressed == 4], 4]},
     Which[TrueQ[pressed == 1], 1, TrueQ[pressed == 2], 2,
      TrueQ[pressed == 3], 3, TrueQ[pressed == 4], 4]]
    }]
  ]
 ]

The sequential overlay presentation was as follows:

The first overlay was a welcome screen with instructions and a "continue" button which was the trigger for the next overlay.

Grid[{
  {Spacer[{70, 50}]},
  {Style["Instructions", FontColor -> fcolor, Bold, FontSize -> 80]},
  {Spacer[{70, 40}]},
  {Style["In the following section, a series of fractions in the form \
a/b with values ranging from 0 to 1 will be presented one at the \
time. Please indicate whether the numerical value of the fraction \
presented is closer to 0 or 1 by pressing either the 0 or 1 buttons \
at the bottom of the screen.", FontColor -> fcolor, FontSize -> 20]},
  {Spacer[{70, 20}]},
  {Style["There will be 10 initial trials which simply require you to \
press either the 0 or 1 buttons when a zero or a one appear on the \
screen. The fraction trials will begin immediately after these \
calibration trials are completed.", FontColor -> fcolor, 
    FontSize -> 20]},
  {Spacer[{70, 20}]},
  {Style["There will be several trials taking only a few seconds \
each. The entire session lasts approximately 5 minutes in total.", 
    FontColor -> fcolor, FontSize -> 20]},
  {Spacer[{70, 20}]},
  {Style["Please make sure your browser window is in fullscreen.", 
    FontColor -> fcolor, FontSize -> 20]},
  {Spacer[{70, 20}]},
  {Style["Press the button below when ready", FontColor -> fcolor, 
    Bold, FontSize -> 40]},
  {Spacer[{70, 20}]},
  {Button[Style["Let the trials begin!", Bold, FontSize -> fsize2],
    DatabinAdd[
     Databin[bin], <|"ID" -> $UserAgentString, 
      "TimeSubmitted" -> DateObject[], "Trial" -> ntrials|>];
    pressed = 2;
    baselineStimuli = 0;
    stimuliPresTime = DateObject[], FrameMargins -> Large
    ]
   },
  {Spacer[{50, 30}]}
  }],

Here is what the code above produced:

When the button is clicked, a time stamp is dropped and the next overlay is triggered. The following overlay contained a loop which simply generated new stimuli and recorded the data upon button presses until a certain number of trials was met.

Grid[{
   {Spacer[{70, 100}]},
   {Style[baselineStimuli, FontColor -> fcolor, FontSize -> fsize, 
     Bold]},
   {Spacer[{70, 80}]},
   {Row
     [{Panel[Button[Style["0", FontSize -> fsize2],
        DatabinAdd[
         Databin[bin], <|"ID" -> $UserAgentString, 
          "Trial" -> baselinecounter, "Stimuli" -> baselineStimuli, 
          "StimuliPresTime" -> stimuliPresTime, 
          "TimeSubmitted" -> DateObject[], "Response" -> "0"|>];
        baselineStimuli = 1;
        pressed = 2;
        baselinecounter++;
        stimuliPresTime = DateObject[], FrameMargins -> 20, 
        Appearance -> "Frameless"
        ]], Spacer[{70, 30}],
      Panel[Button[Style["1", FontSize -> fsize2],
        DatabinAdd[
         Databin[bin], <|"ID" -> $UserAgentString, 
          "Trial" -> baselinecounter, "Stimuli" -> baselineStimuli, 
          "StimuliPresTime" -> stimuliPresTime, 
          "TimeSubmitted" -> DateObject[], "Response" -> "1"|>];
        baselineStimuli = 0;
        pressed = 2;
        baselinecounter++;
        stimuliPresTime = DateObject[], FrameMargins -> 20, 
        Appearance -> "Frameless"
        ]]
      }]},
   {Spacer[{50, 30}]}
   }],
 TrueQ[nbaselinetials == baselinecounter],
 Grid[{
   {Spacer[{70, 100}]},
   {Style[baselineStimuli, FontColor -> fcolor, FontSize -> fsize, 
     Bold]},
   {Spacer[{70, 80}]},
   {Row[{
      Panel[Button[Style["0", FontSize -> fsize2],
        DatabinAdd[
         Databin[bin], <|"ID" -> $UserAgentString, 
          "Trial" -> baselinecounter, "Stimuli" -> baselineStimuli, 
          "StimuliPresTime" -> stimuliPresTime, 
          "TimeSubmitted" -> DateObject[], "Response" -> "0"|>];
        b = RandomInteger[{1, 100}];
        a = RandomInteger[{1, b - 1}];
        pressed = 3;
        stimuliPresTime = DateObject[], FrameMargins -> 20, 
        Appearance -> "Frameless"
        ]], Spacer[{70, 30}],
      Panel[Button[Style["1", FontSize -> fsize2],
        DatabinAdd[
         Databin[bin], <|"ID" -> $UserAgentString, 
          "Trial" -> baselinecounter, "Stimuli" -> baselineStimuli, 
          "StimuliPresTime" -> stimuliPresTime, 
          "TimeSubmitted" -> DateObject[], "Response" -> "1"|>];
        b = RandomInteger[{1, 100}];
        a = RandomInteger[{1, b - 1}];
        pressed = 3;
        stimuliPresTime = DateObject[], FrameMargins -> 20, 
        Appearance -> "Frameless"
        ]]
      }]},
   {Spacer[{50, 30}]}
   }]
 ]

This was used both for a series of practice trials and for the main core of the trials. The practice trials simply require participants to click either the zero or one buttons when a zero or one is presented on the screen. This will be used to create a baseline.

Which[
 TrueQ[counter < ntrials],
 Grid[{
   {Spacer[{70, 50}]},
   {Style[a/b, FontColor -> fcolor, FontSize -> fsize, Bold]},
   {Spacer[{70, 30}]},
   {Row[{
      Panel[Button[Style["0", FontSize -> fsize2],
        DatabinAdd[
         Databin[bin], <|"ID" -> $UserAgentString, "Trial" -> counter,
           "StimuliPresTime" -> stimuliPresTime, 
          "TimeSubmitted" -> DateObject[],
          "Numerator" -> a, "Denominator" -> b, "Response" -> "0"|>];
        b = RandomInteger[{1, 100}];
        a = RandomInteger[{1, b - 1}];
        pressed = 3;
        counter++;
        stimuliPresTime = DateObject[], FrameMargins -> 20, 
        Appearance -> "Frameless"
        ]], Spacer[{70, 30}],
      Panel[Button[Style["1", FontSize -> fsize2],
        DatabinAdd[
         Databin[bin], <|"ID" -> $UserAgentString, "Trial" -> counter,
           "StimuliPresTime" -> stimuliPresTime, 
          "TimeSubmitted" -> DateObject[],
          "Numerator" -> a, "Denominator" -> b, "Response" -> "1"|>];
        b = RandomInteger[{1, 100}];
        a = RandomInteger[{1, b - 1}];
        pressed = 3;
        counter++;
        stimuliPresTime = DateObject[], FrameMargins -> 20, 
        Appearance -> "Frameless"
        ]]
      }]},
   {Spacer[{50, 30}]}
   }],
 TrueQ[counter == ntrials],
 Grid[{
   {Spacer[{70, 50}]},
   {Style[a/b, FontColor -> fcolor, FontSize -> fsize, Bold]},
   {Spacer[{70, 30}]},
   {Row[{
      Panel[Button[Style["0", FontSize -> fsize2],
        DatabinAdd[
         Databin[bin], <|"ID" -> $UserAgentString, "Trial" -> counter,
           "StimuliPresTime" -> stimuliPresTime, 
          "TimeSubmitted" -> DateObject[],
          "Numerator" -> a, "Denominator" -> b, "Response" -> "0"|>];
        pressed = 4, FrameMargins -> 20, Appearance -> "Frameless"
        ]], Spacer[{70, 30}],
      Panel[Button[Style["1", FontSize -> fsize2],
        DatabinAdd[
         Databin[bin], <|"ID" -> $UserAgentString, "Trial" -> counter,
           "StimuliPresTime" -> stimuliPresTime, 
          "TimeSubmitted" -> DateObject[],
          "Numerator" -> a, "Denominator" -> b, "Response" -> "1"|>];
        pressed = 4, FrameMargins -> 20, Appearance -> "Frameless"
        ]]
      }]
    },
   {Spacer[{50, 30}]}
   }]
 ]
,

The last overlay items was a "Thank you for participating" screen.

Grid[{{Spacer[{70, 50}]},
  {Style["You are all done!", FontColor -> fcolor,
    FontSize -> 150, Bold]},
  {Spacer[{70, 50}]},
  {Style["Thank you", FontColor -> fcolor, FontSize -> 150, Bold]}}]

The entire dynamic overlay will be displayed on a notebook. If the entire code is then put on a CloudDeploy function it will create a URL for it to run on a browser. For the most part the web deployed form works just like it does on a notebook. This quick web deploy allows for rapid prototyping of the form.

DataDrop

Note the specifications under the "Button" function.

Button[Style["1", FontSize -> fsize2],
 DatabinAdd[
   Databin[bin], <|"ID" -> $UserAgentString, "Trial" -> counter, 
    "StimuliPresTime" -> stimuliPresTime, 
    "TimeSubmitted" -> DateObject[],
    "Numerator" -> a, "Denominator" -> b, "Response" -> "1"|>];

This essentially logs the data (ID, Trial, StimuliPresTime, TimeSubmitted, Numerator, Denominator, and Response) into a data-bin every time the button is pressed. Adding data directly from the cloud is a nice feature of the Wolfram Data Drop Capabilities. Each time the button is pressed a "New Entry" is logged. This entry can be seen on the Data Drop Website of the bin owner.

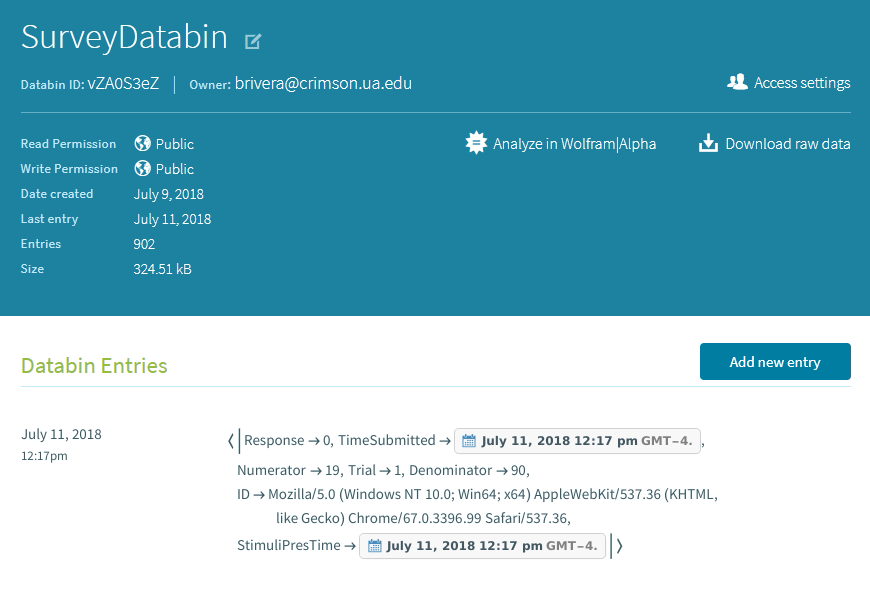
Data Analysis

Databin data can be accessed and manipulated from within a Wolfram notebook. Simply call data bins through their "ID". Below is the code creating a variable "bin" with the contents of data drop bin "vZAOS3eZ" in data set format and selecting only trials with non zero numerators (practice trials were given zero numerators).

    bin = Databin["vZA0S3eZ"];
    surveyData = Dataset[bin];
    filteredData = surveyData[Select[#Numerator > 0 &]]

The dataset format presents the data within the notebook with a nice interface.

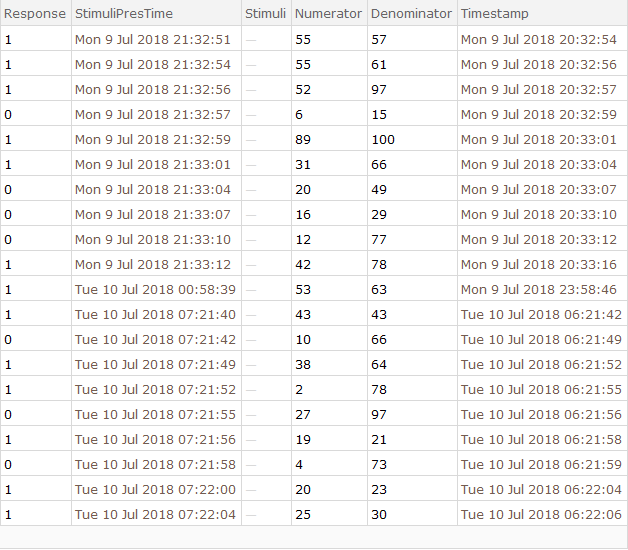
The two columns of time response "StimuliPresTime" and "TimeSubmitted" are used to calculate reaction time. Reaction time will be the time from when the stimuli was presented ("StimuliPresTime") to when the button was clicked (which submits the data to the cloud "TimeSubmitted"). Since time submitted comes later, the stimuli presentation time will be subtracted from it.The result is a list of DateObjets. But these an be transformed into numerical data.

stimuliPresTime = filteredData[All, "StimuliPresTime"];
timeSubmitted =  filteredData[All, "TimeSubmitted"];
DateObjRTs = 
  Table[(timeSubmitted[[i]] - stimuliPresTime[[i]]), {i, 
    Length[stimuliPresTime]}];
RTs = Table[DateObjRTs[[x, 1]], {x, Length[DateObjRTs]}];

In order to calculate the magnitude of each fraction presented, the numerator and denominator columns from the filtered dataset can be extracted.

    numerators = filteredData[All, "Numerator"];
    denominators = filteredData[All, "Denominator"];

The real value magnitude of each fraction (numerator divided by denominator) can be calculated from the numerator and denominator. N forces the value to be presented in real form instead of fraction form. A table with a magnitude and its reaction time for each of the magnitudes and RTs is then created and plotted.

magnitudes = 
  Table[N[numerators[[i]]/denominators[[i]]], {i, Length[numerators]}];
RTbyMag = Table[{magnitudes[[i]], RTs[[i]]}, {i, Length[magnitudes]}];
ListPlot[{RTbyMag}, DataRange -> {0, 1}]

The result of plotting each magnitude from 0 to 1 against the reaction time it takes to specified if it is closer to zero or one is as follows:

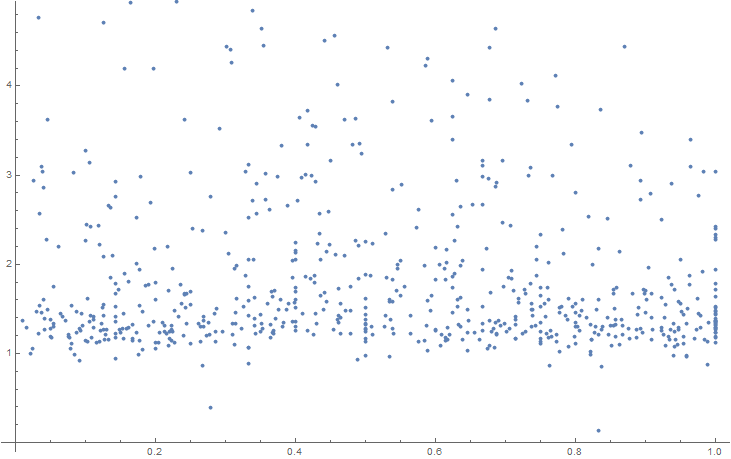
However, the figure above has not filtered incorrect trials. Instead of excluding these, they will be plotted on a different color to see where they are clustering.

Results

The following code sorts correct and incorrect trials.

response = filteredData[All, "Response"];
numberResponse = 
  Table[ToExpression[response[i]], {i, 1, Length[response]}];
Clear[incorrect];
Clear[correct];
correct = {};
Table[Which[
   TrueQ[0.5 > magnitudes[[i]]],
   If[numberResponse[[i]] == 0, 
    AppendTo[correct, {magnitudes[[i]], RTs[[i]]}]]
   ,
   TrueQ[0.5 < magnitudes[[i]]],
   If[numberResponse[[i]] == 1, 
    AppendTo[correct, {magnitudes[[i]], RTs[[i]]}]]
   ], {i, Length[magnitudes]}];
incorrect = {};
Table[Which[
   TrueQ[0.5 > magnitudes[[i]]],
   If[numberResponse[[i]] == 1, 
    AppendTo[incorrect, {magnitudes[[i]], RTs[[i]]}]]
   ,
   TrueQ[0.5 < magnitudes[[i]]],
   If[numberResponse[[i]] == 0, 
    AppendTo[incorrect, {magnitudes[[i]], RTs[[i]]}]]
   ], {i, Length[magnitudes]}];

Finally, we plot the table for correct and incorrect and format the plot for better visibility.

ListPlot[{correct, incorrect}, DataRange -> {0, 1}, 
 PlotLegends -> {Style["Correct", 18, Bold], 
   Style["Incorrect", 18, Bold]}, PlotStyle -> PointSize[.015], 
 AxesLabel -> {Style["Magnitude", Large, Bold], 
   Style["ReactionTime(s)", Large, Bold]}, Filling -> Axis, 
 AxesStyle -> Directive[Black, 25], ImageSize -> 900, 
 Ticks -> {{.1, .2, .3, .4, .5, .6, .7, .8, .9, 1}, {1, 2, 3, 4, 5, 
    6}}]

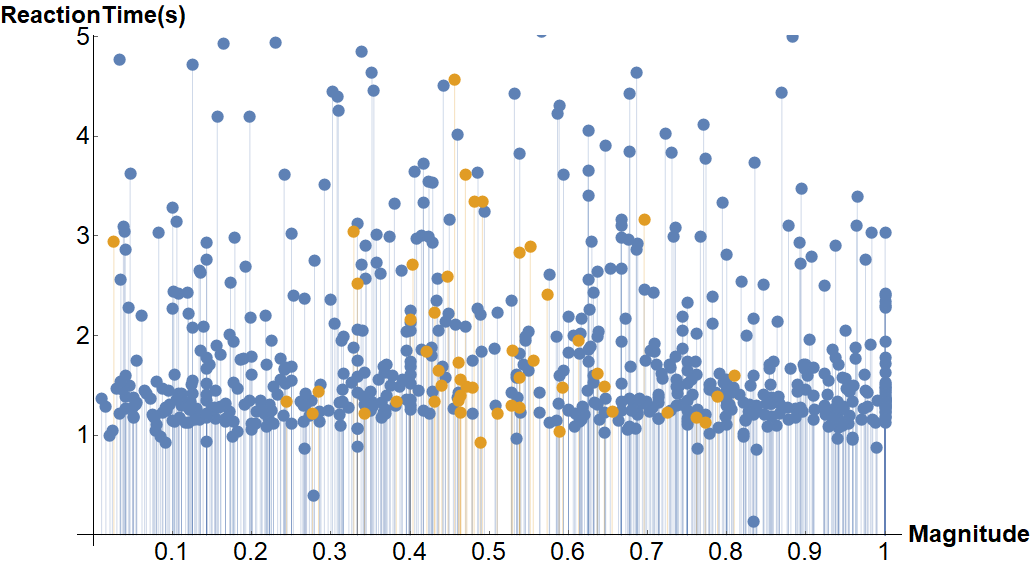
From the few hundred trials collected, a nice plot of reaction time (RT) in seconds over numerical magnitude (zero to one) can be created plotting correct and incorrect trials in different colors.

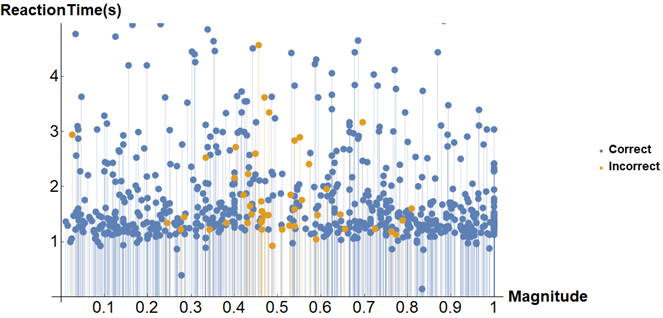
From the plot above, an average response time cluster just above 1000 milliseconds can be seen. This makes visible the clustering of errors around .5. As expected, for the simple task of judging the magnitude of a fraction between 0 and 1, it becomes more difficult to correctly judge the ratio between numerator and denominator as they approximate in value.

Future Work

The experiment above still needs to be further developed to be compatible across different web browsers and on mobile. There were a couple of web connectivity delays and incompatibilities when it was ran on certain browsers.

Future experiments will adapt this paradigm to study additional numerical cognition processes such as problem solving and graph interpretation. There are many additional cognitive tasks that can be studied using the Wolfram language's cloud deploy capabilities such as reading/ language processing and visual/audio recognition tasks. Additionally, the showcased web deploy capabilities can be used by educators for live assessment.