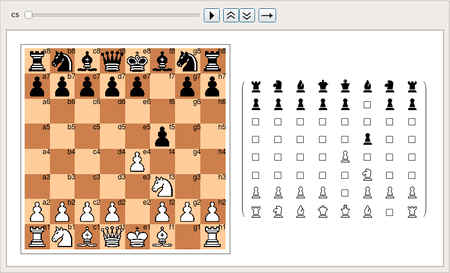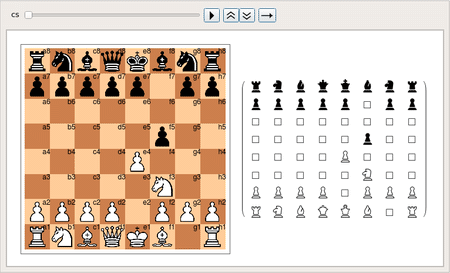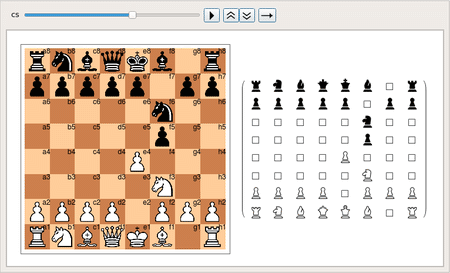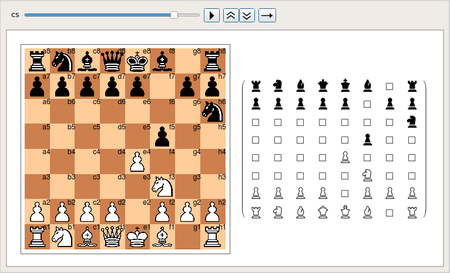
Summary & Objectives

The rules of chess have been perfected for more than a millennia to ensure an exciting game every time. These relatively simple rules are capable of producing very interesting and complex dynamics that deserve to be studied in their own rights, not just merely for competition purposes. This project aims at laying down the formalism to capture the game of chess as well as many other board and card games. In accordance with this formalism, a Mathematica chess package has been developed which creates, displays, and evolves a ChessState object using ChessState, ChessPlot, and ChessEvolve functions.

ChessPlot enables the user to provide options such as setting board color set, displaying coordinates, rotating point of view, or extracting MatrixForm of a ChessState.

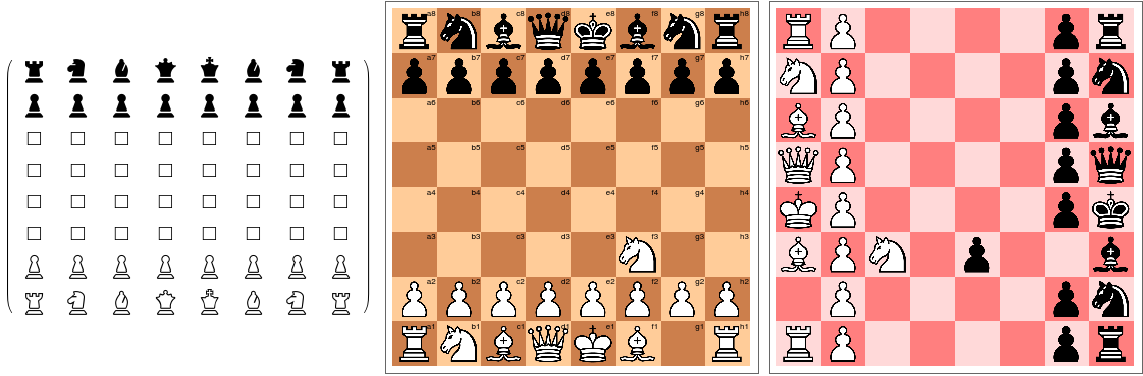
In addition, a list of rule functions is provided which take in a ChessState and output all the possible moves in accordance with the rule they represent.

With this setup, the user is able to setup any ChessEvaluate function and explore the chess space. This open-ended chess design also enables the user to modify the rules with ease so they can explore chess variations such as antichess, atomic chess, and others (see LiChess.org for more examples).

ChessState

Many board/card games may be represented using an association where coordinates in the game are associated with states. Specifically for chess, we can write:

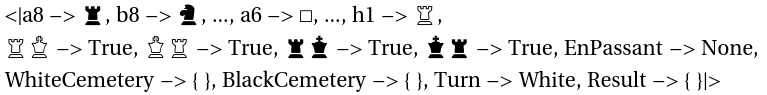
Which can be encapsulated in a wrapper for aesthetic reasons as well as additional functionalities that help the user to extract the state of a coordinate using different notations (e.g. "e1", {rank, file} = {1, 5}).

In order to avoid referring to previous states of the game, auxiliary (as in not part of the board) has been added. For instance, if a pawn may be captured via En passant, it's coordinate will be mentioned. As another example, if the rooks or the king move, the opportunity of castling will be revoked. White and black cemeteries are there to keep track of captured pieces. Turn switches between White and Black after each move. The game ends when the Result is set to "1/2-1/2", "1-0", or "0-1".

A Move $=$ A Set of Actions

A move is a list of actions. For instance, the move of a white pawn at a7 capturing a rook at b8 and becoming a queen may be represented as {a7 → ♔ , ♜ → BlackCemetery, b8 → ♕ }.

Mathematical Formulation of Chess Rules

If we want to develop a chess algorithm, we should list all the rules pseudo-mathematically as such:

(Forgive me for mistakes and for using an image instead of typing it. I will try to write this up more clearly at a later time)

Game Rules $=$ Exhaustive Move Generators

I have used the rules expressed above to create functions that intake a ChessState and output all the possible moves in accordance with the rules. For instance, an exhaustive move generator for knights in Mathematica would look like this:

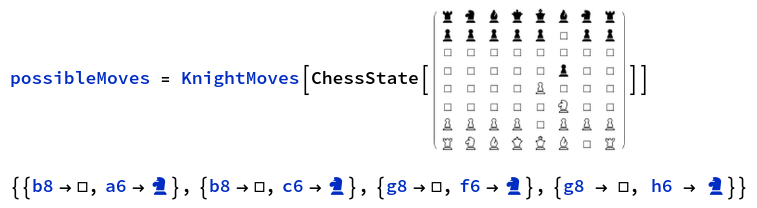
Be aware that not all rules might have been implemented as of the time you are reading this post.

Code on GitHub

You can find my code on GitHub. You can either import chess.m as a package or use Notebook01.nb for code, documentation, and demonstrations. The following is the link to GitHub but be aware that I am planning to move this to a new GitHub location (before Jan 2019). If that happens, I'll update this link.

https://github.com/Miladiouss/Summer2018Starter/tree/master/ChessPackage