Exploration of Fundamental Mathematics, via Implementation of Common Axiom Systems and Proof Generation
Utilizing the function FindEquationalProof introduced in version 11.3 of Mathematica, I implemented and proved common algebraic and logical conjectures as well as hypothetical, but plausible combinations of axioms and conjectures, as introduced in Chapter 12, Section 9 of Stephen Wolfram's book, A New Kind of Science. The Full Computational Essay is attached at the bottom.
This post is divided into the following 4 sections:
- Implementation of Modern Axiom Systems
- Proof Generation
- Alternative Axiom Systems
- Implications
Implementation of Modern Axiom Systems
Axioms, Conjectures, Theorems and Proofs
Most common math curriculums prioritize the introduction of theorems, but not many take the time to properly prove each of them. A mathematical proof is a logical argument for the validity of a particular statement. A statement without proof is called a conjecture. A statement that has been proved is a theorem.
Such mathematical system of proofs build upon each other. A proof might require another theorem, which might require another theorem for its proof. When we continue this trace of proofs and theorems, we reach a point in which a statement is so obviously true that it needs no proof. This is the informally defined axiom.
An example of an axiom may be a + b == b + a, or Not[True] == False. Despite the simplicity of these statements, without a consistent set of enough axioms, it is impossible to build up a viable system of mathematics.
A more complete definition, as well as the history of the investigation of proofs, can be found in the following Wikipedia article:
Wikipedia - Proof Theory
The FindEquationalProof Function
This newly-implemented function, though rather lacking in practicality, is conceptually an interesting product, as it introduces a method of computationally generating human-readable (but possibly lengthy) proofs. It is also interesting in that a system of axioms can be specified, rather than implied, which allows for the possibility of limiting the range of axioms a proof can use, or providing a completely new system of axioms, separate from that of our mathematics.
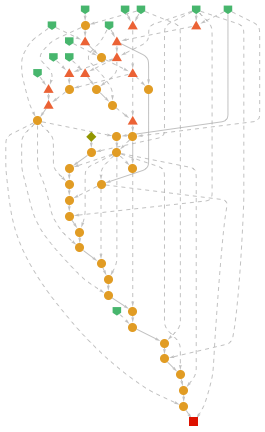
The function, in essence, generates such proofs by simple substitutionit replaces a part of an expression by the rules of the axiom, or lemmas (also generated via the same method). The following diagram excerpted from Wolfram's book visualizes the algorithm:
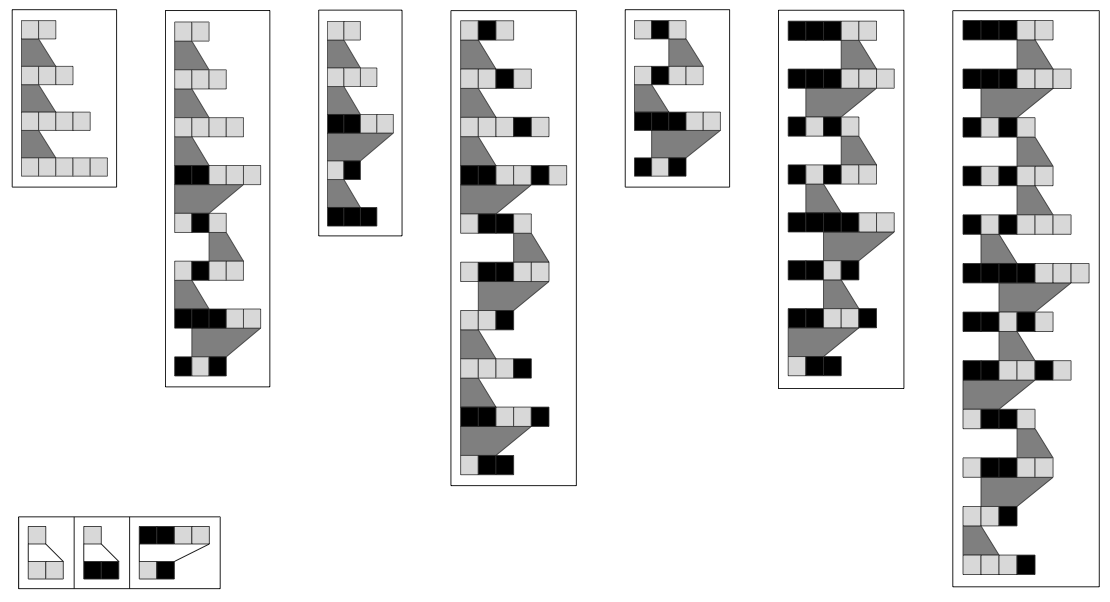 [1]
[1]
Axioms listed in the bottom left are used in the proofs of theorems. The validity of a particular statement is therefore proved by investigating if a certain set of substitutions to one expression can be transformed into another.
This process is equivalent to the proofs of conjectures of mathematics. Every proof is merely a series of substitution of parts of statements with axioms (or lemmas derived from axioms). Given enough computational power, and more importantly, a required set of consistent axioms, a theorem can be proved.
Providing definitions and axioms
The only statements the FindEquationalProof function can understand, according to the documentation, are:
- lhs==rhs equational logic
- ForAll[vars,lhs==rhs] universal quantifiers over equational logic identities
Implementing even the simplest axioms were, therefore, a notoriously time-consuming task.
definitions = {
ForAll[{a, b}, ex[a, b] == not[ForAll[{a}, not[b]]]],
ForAll[{a, b}, im[a, b] == or[not[a], b]],
ForAll[{a}, ueq[a, a] == not[eq[a, a]]],
ForAll[{a, b}, eqv[a, b] == and[im[a, b], im[b, a]]],
ForAll[{a, b}, nand[a, b] == not[and[a, b]]],
ForAll[{a, b}, xor[a, b] == and[or[a, not[b]], or[not[a], b]]],
ForAll[{a, b}, or[or[a, b], not[b]] == "T"],
not["T"] == "F",
ForAll[{a}, eq[a, a] == "T"],
ForAll[{a, b}, im[a, b] == or[not[a], b]]
};
booleanLogic = {
ForAll[{a, b}, and[a, b] == and[b, a]],
ForAll[{a, b}, or[a, b] == or[b, a]],
ForAll[{a, b}, and[a, or[b, not[b]]] == a],
ForAll[{a, b}, or[a, and[b, not[b]]] == a],
ForAll[{a, b, c}, and[a, or[b, c]] == or[and[a, b], and[a, c]]],
ForAll[{a, b}, or[a, and[b, c]] == and[or[a, b], or[a, c]]]
};
Simple Boolean algebra axioms are specified, providing the system to compute And, Or, and Not operations. Definitions not provided, like Exists, Implies, !=, or <-> must be defined using only these logical operators. Notable implementations include:
ForAll[{a,b},ex[a,b]==b]] (*Definition of Existance*)
ForAll[{a, b}, im[a, b] == or[not[a],b] (*Definition of Implication*)
ForAll[{a, b}, or[ or[a,b], not[b] ] == "T"] (*Definition of Truth*)
ForAll[{a, b}, eq[a, b] == "T"] (*Functional Definition of Equality*)
More complicated operations such as NAND or XOR are defined as combinations of these operations.
Using these definitions and axioms, we can prove simple logical theorems, such as De Morgan's law, or the Modus Ponens. The output Proof Graphs show the Axioms in Green, and Lemmas in Red and Orange, revealing the order and steps of the proof:
modusP = ForAll[{p, q}, im[and[im[p, q], p], q] == "T"];
deMorgan = ForAll[{a, b}, not[and[a, b]] == or[not[a], not[b]]];
axioms = Join[definitions, booleanLogic];
FindEquationalProof[modusP, axioms]["ProofGraph"]
FindEquationalProof[deMorgan, axioms]["ProofGraph"]
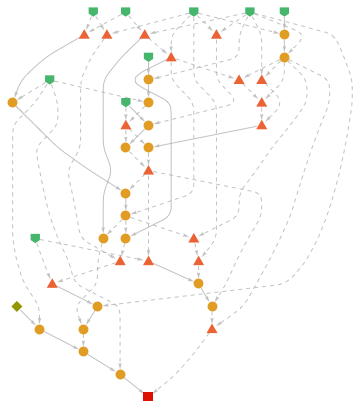
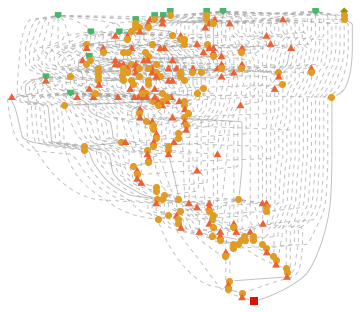
Note the fact that even such simple proofs can take over 200 steps to prove from the systems of axioms. More complicated expressions, such as the Wolfram Axiom, can be shown to follow from these axioms:
wolframLogic =
ForAll[{a, b, c},
nand[nand[nand[a, b], c], nand[a, nand[nand[a, c], a]]] == c];
FindEquationalProof[wolframLogic, axioms]["ProofGraph"]
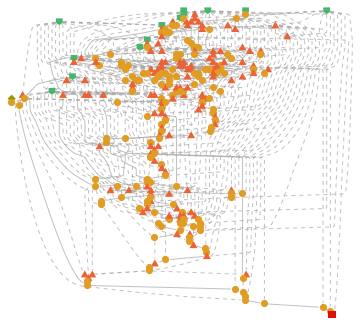
Another notable fact is that despite the length of the Wolfram Axiom compared to De Morgan's law, it takes a similar number of steps to reach the proof. A possible justification may be related to the Principle of Computational Equivalence.
Implementing Arithmetic
The first attempted implementation of arithmetic was using a modified version of Peano's axioms. His system is simple to implement, but is slightly harder to express. 0 is defined, and all natural numbers are defined using a successor function s[x], which is equivalent to adding 1 to x, e.g. 1==s[0],2==s[s[0]], and so on. Addition is defined as a recursive function of s, and multiplication is defined as a recursive function of addition. Note that the distributive and commutative properties of addition and multiplication is not defined originally in Peano's axioms.
arithmetic = {
(*Addition*)
ForAll[{x, y}, add[x, s[y]] == s[add[x, y]]],
ForAll[{x}, add[0, x] == x],
ForAll[{x, y}, add[x, y] == add[y, x]],
ForAll[{x, y, z}, add[x, add[y, z]] == add[add[x, y], z]],
(*Multiplication*)
ForAll[{x, y}, times[x, s[y]] == add[times[x, y], x]],
ForAll[{x}, times[0, x] == 0],
ForAll[{x}, times[x, s[0]] == x],
ForAll[{x, y}, times[x, y] == times[y, x]],
ForAll[{x, y}, times[x, times[y, z]] == times[times[x, y], z]],
ForAll[{x, y, z},
add[times[x, z], times[y, z]] == times[add[x, y], z]]
};
With these in hand, many simple algebraic properties can be proved: 1+2x+x*x == (1+x)(1+x)
distribution =
ForAll[{x},
add[s[0], add[times[s[s[0]], x], times[x, x]]] ==
times[add[s[0], x], add[s[0], x]]];
FindEquationalProof[distribution, arithmetic]["ProofGraph"]
We can further extend this system by defining powers.
powers = {
ForAll[{x}, pow[x, s[0]] == x],
ForAll[{x}, pow[x, 0] == 1],(*Note: 0^0 is undef*)
ForAll[{x, y}, pow[x, s[y]] == times[pow[x, y], x]],
ForAll[{x, y, z}, pow[pow[x, y], z] == pow[x, times[y, z]]
]};
arithmetic = Join[arithmetic, powers];
However, if we introduce negative numbers, the system generates an impossible proof:
negatives = {
ForAll[{x}, add[x, neg[x]] == 0],
ForAll[{x}, y, sub[x, y] == add[x, neg[y]]]
};
arithmetic = Join[arithmetic, negatives];
zeroEqualsOne = FindEquationalProof[0 == s[0], arithmetic]
zeroEqualsOne["ProofNotebook"];
(*Remove semicolon and evaluate to view proof notebook*)
Inspection of the Proof Notebook reveals that the problem is due to the undefined power of 0^0. As x^0 is defined as 1, but 0^x is defined as 0, the inevitable conclusion is that 0 is equal to 1.
This problem showcases the importance of defining a sturdy set of axioms. Although this problem can be eliminated by the use of the "[Implies]" operator defined in Boolean logic, it would be more wise to follow the steps of previous mathematicians, rather than to continue building a new set of axioms, as unpredictable inconsistencies and contradictions may occur.
Real Algebra and Tarski Axioms
To implement real algebra, a more robust set of axioms need to be defined. Tarski's axioms of real arithmetic are what many consider to be the basis of current algebra:
 [1]
[1]
Before we do so, however, axioms from predicate logic, such as implication or equivalence, are also required.
predicateLogic = {
im[ForAll[{a}, im[b, c]], im[ForAll[{a}, b], ForAll[{b}, c]]] ==
"T",
im[fq[a, b], im[a, ForAll[{b}, a]]] == "T",
im[fq[b, a], ex[a, eq[a, b]]] == "T"
};
tarskiAxioms = {
ForAll[{x, y, z}, add[x, add[y, z]] == add[add[x, y], z]],
ForAll[{a}, add[a, 0] == a],
ForAll[{a}, add[a, neg[a]] == 0],
ForAll[{a, b}, add[a, b] == add[b, a]],
ForAll[{x, y, z}, times[x, times[y, z]] == times[times[x, y], z]],
ForAll[{x, y, z},
add[times[x, z], times[y, z]] == times[add[x, y], z]],
ForAll[{x, y}, times[x, y] == times[y, x]],
ForAll[{a}, times[a, 1] == a],
ForAll[{a}, im[ueq[a, 0], eq[times[a, rec[a]], 1]] == "T"],
ForAll[{a, b, c}, im[and[gt[a, b], gr[b, c]], gr[a, c]] == "T"],
ForAll[{a, b}, im[gr[a, b], ueq[a, b]] == "T"],
ForAll[{a, b}, or[gr[a, b], a] == or[b, gr[b, a]]],
ForAll[{a, b, c}, im[gr[a, b], gr[add[a, c], add[b, c]]] == "T"],
ForAll[{a, b, c},
im[and[gr[a, b], gr[c, 0]], gr[times[a, c], times[b, c]]] ==
"T"],
gr[1, 0] == "T"
};
axioms = Join[definitions, booleanLogic, predicateLogic,
tarskiAxioms];
With these, we can compute with the set of all real numbers. Proving again the distribution law, and investigating the Proof Notebook, reveals the use of reciprocals, negative numbers, and even fractions in the proof.
distribution =
ForAll[{a, b, x, y},
times[add[x, y], add[x, b]] ==
add[add[times[x, x], times[b, x]], add[times[x, y], times[b, y]]]];
FindEquationalProof[distribution, axioms]["ProofNotebook"];
(*remove semicolon and evaluate to inspect ProofNotebook*)
It is surreal to see that the whole of algebra can be defined in these few axioms. Stephen Wolfram, in his book, remarks on this fact as well, stating after the two-page list of mathematical axioms that "It is from these axiom systems [...] that most of the millions of theorems in the literature of mathematics have ultimately been derived."
Proof Generation
Elimination of Axioms
A natural extension of such an investigation would be to computationally determine how many axioms could be eliminated from a particular proof. A grid would be ideal to view such data, therefore a wrapper function was written in order to automate this process.
generateProof accepts a list of theorems and axioms, and returns a 2-D array of its proofObjects. generateGrid accepts a list of theorems and axioms, as well as a few options about its display, and outputs a grid, revealing the number of steps of each proof.
generateProof[thms_?ListQ, axms_?ListQ, perTimeConstraint_?IntegerQ] :=
Module[{},
Table[Table[
FindEquationalProof[ForAll[{a, b, c}, thm], axm,
TimeConstraint -> perTimeConstraint], {thm, thms}], {axm, axms}]]
generateGrid[thms_?ListQ, axms_?ListQ, AxiomLength_?IntegerQ,
TimeConstraint_?IntegerQ, scheme_?StringQ, SimpleLabels_?BooleanQ] :=
Module[{proofs, steps, labels, viewThems, viewSteps, colorRules},
proofs = generateProof[thms, axms, TimeConstraint];
steps =
Table[StringCount[ToString@#["ProofFunction"], ";"] & /@
proofs[[n]], {n, Length[proofs]}];
labels = (Rest@Subsets@Range[AxiomLength]);
viewThems = {"Theorems"}~Join~thms;
viewSteps =
Table[{If[SimpleLabels, labels[[n]], axms[[n]]]}~Join~
steps[[n]], {n, Length[proofs]}];
{Rotate[#, \[Pi]/2, Baseline, {1, 1}] & /@ viewThems}~Join~steps;
colorRules = {None, None}~
Join~{Flatten@
Table[Table[{y, x} ->
ColorData[scheme,
Rescale[steps[[y - 1]][[x - 1]], {0,
Max@Flatten@steps}]], {x, 2, Length[steps[[1]]] + 1}], {y,
2, Length[steps] + 1}]};
Grid[{Rotate[#, \[Pi]/2] & /@ viewThems}~Join~viewSteps,
ItemSize -> {{Automatic, Table[1, Length[steps] - 1]}, {Automatic,
Table[1, Length[axms] - 1]}}, Spacings -> Automatic,
Frame -> All, Alignment -> Left, Background -> colorRules]]
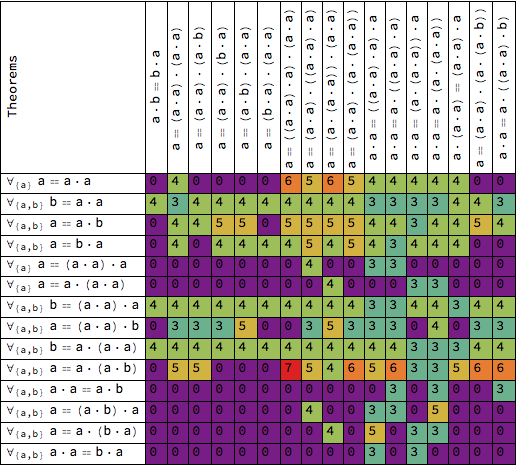
For example, a set of randomly-generated axioms proving a set of equally randomly-generated theorems might look like the following gridthe top row are the theorems, and the leftmost column are the axioms. Each square is numbered and colored according to the length of its proof:
In the our case, the intent is to investigate how many axioms from Boolean logic we can remove to prove particular theorems. Therefore, we can provide the generateGrid function a list of subsets of the Boolean logic. Each subset still requires definitions for things such as implication or equals, so it is prepended to each list.
subsets = Rest@Subsets@booleanLogic;
Short[subsets, 5]
Out: $$\left\{\left\{\forall _{\{a,b\}}\text{and}(a,b)=\text{and}(b,a)\right\},\left\{\forall _{\{a,b\}}\text{or}(a,b)=\text{or}(b,a)\right\},\langle\langle 60\rangle\rangle ,\left\{\forall _{\{a,b\}}\text{and}(a,b)=\text{and}(b,a),\forall _{\{a,b\}}\text{or}(a,b)=\text{or}(b,a),\forall _{\{a,b\}}\text{and}(a,\text{or}(b,\text{not}(b)))=a,\forall _{\{a,b\}}\text{or}(a,\text{and}(b,\text{not}(b)))=a,\forall _{\{a,b,c\}}\text{and}(a,\text{or}(b,c))=\text{or}(\text{and}(a,b),\text{and}(a,c)),\forall _{\{a,b,c\}}\text{or}(a,\text{and}(b,c))=\text{and}(\text{or}(a,b),\text{or}(a,c))\right\}\right\}$$
subsetAxioms = Join[definitions, #] & /@ (Rest@Subsets@booleanLogic);
Short[subsetAxioms, 6]
$$\left\{\left\{\forall _{\{a,b\}}\text{ex}(a,b)=\text{not}(\text{not}(b)),\forall _{\{a,b\}}\text{im}(a,b)=\text{or}(\text{not}(a),b),\forall _a\text{ueq}(a,a)=\text{not}(\text{eq}(a,a)),\forall _{\{a,b\}}\text{eqv}(a,b)=\text{and}(\text{im}(a,b),\text{im}(b,a)),\forall _{\{a,b\}}\text{nand}(a,b)=\text{not}(\text{and}(a,b)),\forall _{\{a,b\}}\text{xor}(a,b)=\text{and}(\text{or}(a,\text{not}(b)),\text{or}(\text{not}(a),b)),\forall _{\{a,b\}}\text{or}(\text{or}(a,b),\text{not}(b))=\text{T},\text{not}(\text{T})=\text{F},\forall _a\text{eq}(a,a)=\text{T},\forall _{\{a,b\}}\text{im}(a,b)=\text{or}(\text{not}(a),b),\forall _{\{a,b\}}\text{and}(a,b)=\text{and}(b,a)\right\},\langle\langle 61\rangle\rangle ,\left\{\forall _{\{a,b\}}\text{ex}(a,b)=\text{not}(\text{not}(b)),\langle\langle 14\rangle\rangle ,\forall _{\{a,b,c\}}\text{or}(a,\text{and}(b,c))=\text{and}(\text{or}(a,b),\text{or}(a,c))\right\}\right\}$$
After such formatting, the list subsetAxioms contains every combination of axioms, each with the list of definitions. As displaying such long expressions on the grid is infeasible, we can number each axiom of Boolean logic, and only show its index on the grid. In the following example we investigate the provability and the number of steps required for proving De Morgan's theorem, using subsets of Boolean logic. The output grid is edited for easy viewing.
booleanLogic = {
(*1*) ForAll[{a, b}, and[a, b] == and[b, a]],
(*2*) ForAll[{a, b}, or[a, b] == or[b, a]],
(*3*) ForAll[{a, b}, and[a, or[b, not[b]]] == a],
(*4*) ForAll[{a, b}, or[a, and[b, not[b]]] == a],
(*5*) ForAll[{a, b, c}, and[a, or[b, c]] == or[and[a, b], and[a, c]]],
(*6*) ForAll[{a, b}, or[a, and[b, c]] == and[or[a, b], or[a, c]]]
};
generateGrid[{deMorgan}, subsetAxioms, 6, 10, "Rainbow", True]

Generation of Random Boolean Expressions and Proofs
In order to see what proofs are required for particular theorems, we need to be able generate these theorems repetitively. The first function, replacer, translates the Wolfram Language's native Heads (e.g. Or, And, Nand, True), with ones defined within the axiom set (e.g. or, and, nand, "T"). The second function, randomBoolExp, generates a single logical statement in the axiom set's language.
replacer[expr_, reverse_?BooleanQ] :=
Module[{dictionary, reverseDictionary},
dictionary = {"and" -> "And", "or" -> "Or", "not" -> "Not",
"ex" -> "Exists", "im" -> "Implies", "ueq" -> "Unequal",
"eq" -> "Equal", "eqv" -> "Equivalent", "nand" -> "Nand",
"T" -> "True", "F" -> "False", "x" -> "X", "add" -> "Plus",
"times" -> "Times"};
Needs["GeneralUtilities`"];
reverseDictionary =
Association[dictionary] // AssociationInvert // Normal;
ToExpression@
StringReplace[ToString@expr,
If[reverse, reverseDictionary, dictionary]]]
randomBoolExp[numb_?IntegerQ, form_?StringQ] :=
Module[{tripleDictionary, replBoolExp, shortBoolExp},
tripleDictionary = {or[x_, y_, z_] -> or[x, or[y, z]],
and[x_, y_, z_] -> and[x, and[y, z]],
nand[x_, y_, z_] -> not[and[x, and[y, z]]],
xor[x_, y_, z_] -> and[and[a, b, c], not[and[a, b, c]]]};
replBoolExp =
replacer[
FullForm@(randBoolExp =
BooleanFunction[RandomInteger[1, 2^numb],
ToExpression /@ Alphabet[][[;; numb]]]), True] //.
tripleDictionary;
shortBoolExp =
replacer[FullForm@BooleanMinimize[randBoolExp, form], True] //.
tripleDictionary;
replBoolExp == shortBoolExp]
randomBoolExp[3, "NAND"](*Repeatedly evaluate for different output*)
Out:
or[and[a,and[not[b],c]],and[not[a],and[not[b],not[c]]]]==nand[not[and[a,and[not[b],c]]],not[and[not[a],and[not[b],not[c]]]]]
The function generates the expression via a random integer generator which is used as a truth table for the built-in BooleanFunction function. Each variable in the expression is an alphabet, and the number of variables are adjusted with the variable numb, which defaults to {a,b,c}. The expression is then simplified using a specific form, e.g. "NAND", "ANF", etc., and equated with the original equation. Finally, the expression is translated into the axiom's language set.
expressions = {ForAll[{a, b, c},
or[and[not[a], not[b]], or[and[not[a], c], and[not[b], not[c]]]] ==
or[and[not[a], c], and[not[b], not[c]]]],
ForAll[{a, b, c},
or[and[a, not[b]], or[and[not[a], b], and[b, not[c]]]] ==
or[and[a, not[b]], or[and[a, not[c]], and[not[a], b]]]],
ForAll[{a, b, c},
or[and[a, b], or[and[not[a], not[b]], and[b, c]]] ==
or[and[a, b], or[and[not[a], not[b]], and[not[a], c]]]],
ForAll[{a, b, c},
or[and[not[a], not[b]], or[and[b, c], and[not[b], not[c]]]] ==
or[and[not[a], c], or[and[b, c], and[not[b], not[c]]]]]
};
expressions = {ForAll[{a, b, c},
or[and[not[a], not[b]], or[and[not[a], c], and[not[b], not[c]]]] ==
or[and[not[a], c], and[not[b], not[c]]]],
ForAll[{a, b, c},
or[and[a, not[b]], or[and[not[a], b], and[b, not[c]]]] ==
or[and[a, not[b]], or[and[a, not[c]], and[not[a], b]]]],
ForAll[{a, b, c},
or[and[a, b], or[and[not[a], not[b]], and[b, c]]] ==
or[and[a, b], or[and[not[a], not[b]], and[not[a], c]]]],
ForAll[{a, b, c},
or[and[not[a], not[b]], or[and[b, c], and[not[b], not[c]]]] ==
or[and[not[a], c], or[and[b, c], and[not[b], not[c]]]]]
};
defAxioms = Join[definitions, #] & /@ (Rest@Subsets@booleanLogic);
grid = generateGrid[expressions, defAxioms, 6, 20, "Rainbow", True]
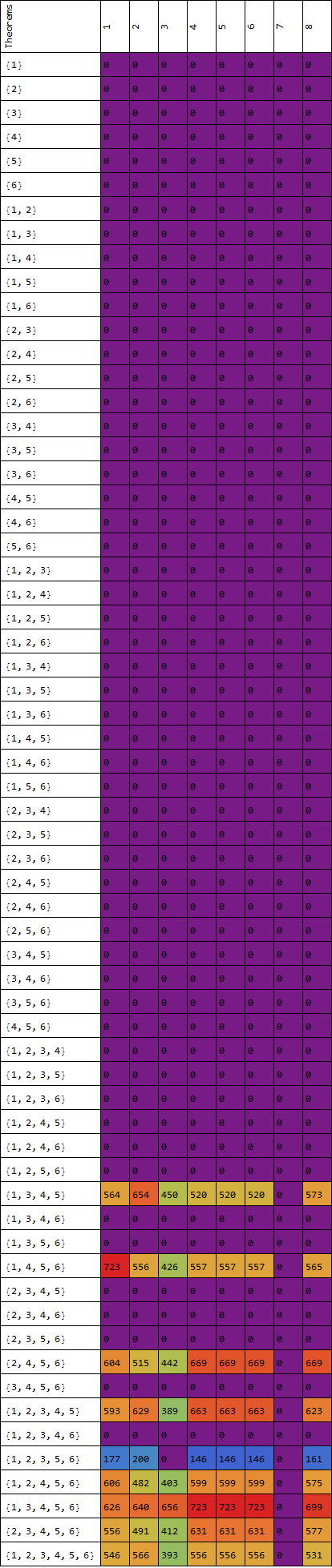
The empty columns for the 7th theorem is believed to be an issue of computing; limited computed power necessitated the time constraint of 20 seconds per proof.
An interesting fact to denote is that most of the generated expressions were provable without the full set of axioms. One would normally expect only a complete axiom system to be able to prove or falsify a statement. Despite the simplicity of these theorems compared to the complex mathematical problems researched in the real world, we can see that it is very plausible to generate proofs without a complete axiom system. It is actually the case that there can be no complete set of axioms, as an arbitrary number of axioms with arbitrary operators can be generated (as explored in the following section). It would also be possible to draw a relation with Gödel's Incompleteness theorem, which suggests that no consistent, complete set of axioms exist that can prove all possible truths describable within the system. A civilization which only considers the {1,2,3,5,6} without the 4th axiom, might be able to express the 3rd theorem, but would not be able to prove it without expanding its axiom system.
Alternative Axiom Systems
A new operator
Our common sense tells us that our system of axioms, i.e., logic, is the only possible system of axioms that exists. However, this is not necessarily the case. An expression can be created with an arbitrary operator, and those expressions can be tried as axioms or theorems, despite not being representable with our system.
Let us imagine a new operator, "$\cdot$", the CenterDot. We can then introduce variables, a and b, to build up expressions like the following:
$$((b\cdot (a\cdot a))\cdot a)\cdot b=a$$
This is impossible to make sense of within our system of logic, but still is a valid expression that describes an equation. Whether it is understandable or not is an unrequited issue; a more interesting question would be if these systems are viable, which we will explore by using them to prove other theorems.
The following list defines some of these arbitrary equalities that constitute as valid expressions:
$$\text{imaginaryAxioms}=\{\\a=a,b=a,a\cdot a=a,a\cdot b=a,\\b\cdot a=a,b\cdot b=a,a\cdot b=b\cdot a,a\cdot (a\cdot a)=a,\\(a\cdot a)\cdot a=a,a\cdot (a\cdot b)=a,a\cdot (b\cdot b)=a,b\cdot (a\cdot a)=a,\\b\cdot (a\cdot b)=a,b\cdot (b\cdot a)=a,(a\cdot a)\cdot b=a,(a\cdot b)\cdot a=a,\\(a\cdot b)\cdot b=a,(b\cdot a)\cdot a=a,(b\cdot a)\cdot b=a,(b\cdot b)\cdot a=a,\\b\cdot (b\cdot b)=a,(b\cdot b)\cdot b=a,(a\cdot a)\cdot (a\cdot a)=a,a\cdot ((a\cdot a)\cdot b)=a,\\(a\cdot a)\cdot (a\cdot b)=a,(a\cdot b)\cdot (b\cdot c)=a,(a\cdot b)\cdot c=a\cdot (b\cdot c),((b\cdot b)\cdot a)\cdot (a\cdot b)=a,\\((b\cdot (a\cdot a))\cdot a)\cdot b=a,b\cdot (c\cdot (a\cdot (b\cdot c)))=a,(a\cdot b)\cdot (a\cdot (b\cdot c))=a,(((b\cdot a)\cdot c)\cdot a)\cdot (a\cdot c)=a,(((b\cdot c)\cdot d)\cdot a)\cdot (a\cdot d)=a,\\\{(a\cdot b)\cdot a=a,a\cdot a=b\cdot b\},\{(a\cdot a)\cdot (a\cdot a)=a,a\cdot b=b\cdot a\},\\(b\cdot (b\cdot (a\cdot a)))\cdot (a\cdot (b\cdot c))=a\};$$
Similarly, as we did in the previous section with Boolean algebra, we can generate theorems to evaluate what these axioms can prove. The task is done with the following function randThms, and its related functions: [2]
canonicalize[list_] :=
DeleteDuplicates[
DeleteDuplicates[Sort /@ list, #1 === (#2 /. {1 -> 0, 0 -> 1}) &]]
canonicalize[list_, vars_] :=
DeleteDuplicates[
DeleteDuplicates[Sort /@ list,
Function[{x, y},
MatchQ[x,
Alternatives @@ ((y /. (Rule @@@
Partition[Append[#, First[#]], 2, 1])) & /@
Permutations[vars])]]]]
revariable[expr_] := (expr /. {0 -> a, 1 -> b, 2 -> c})
randThms[length_?IntegerQ] :=
Module[{thms, axms, newthms, newaxms, ns},
thms = Cases[
Apply[Equal, #] & /@
Flatten[Groupings[#, CenterDot -> 2] & /@
Table[Rest[IntegerDigits[ns, 2]], {ns, length}]], _Equal];
newthms =
Select[revariable[canonicalize[thms]],
TautologyQ[Equivalent @@ (# /. CenterDot -> Nand)] &]
]
For example,
randThms[50] // Column
Out:
$$\begin{array}{l} a\cdot b=b\cdot a \\ a=(a\cdot a)\cdot (a\cdot a) \\ a=(a\cdot a)\cdot (a\cdot b) \\ a=(a\cdot a)\cdot (b\cdot a) \\ a=(a\cdot b)\cdot (a\cdot a) \\ a=(b\cdot a)\cdot (a\cdot a) \\ \end{array}$$
Arbitrary Proofs
Using the above mentioned proofGrid function, we can visualize which axioms yield which theorems. As in the previous run, the axioms and theorems are numbered for visual clarity. Again, despite the fact that it is always impossible to determine if a certain theorem holds, the simplicity of the ones used allow for an acceptable level of confidence.
$$\text{imaginaryTheorems}=\{a\cdot b=b\cdot a,a=(a\cdot a)\cdot (a\cdot a),a=(a\cdot a)\cdot (a\cdot b),a=(a\cdot a)\cdot (b\cdot a),a=(a\cdot b)\cdot (a\cdot a),a=(b\cdot a)\cdot (a\cdot a),a=((a\cdot a)\cdot a)\cdot (a\cdot a),a=(a\cdot a)\cdot ((a\cdot a)\cdot a),a=(a\cdot (a\cdot a))\cdot (a\cdot a),a=(a\cdot a)\cdot (a\cdot (a\cdot a)),a\cdot a=((a\cdot a)\cdot a)\cdot a,a\cdot a=a\cdot ((a\cdot a)\cdot a),a\cdot a=(a\cdot (a\cdot a))\cdot a,a\cdot a=a\cdot (a\cdot (a\cdot a)),a\cdot (a\cdot a)=(a\cdot a)\cdot a,a=(a\cdot a)\cdot (a\cdot (a\cdot b)),a\cdot a=a\cdot ((a\cdot a)\cdot b),a=(a\cdot a)\cdot ((a\cdot b)\cdot a),a=(a\cdot a)\cdot (a\cdot (b\cdot a)),a\cdot a=((a\cdot a)\cdot b)\cdot a,a=(a\cdot a)\cdot (a\cdot (b\cdot b)),a\cdot a=a\cdot ((a\cdot b)\cdot b),a=(a\cdot a)\cdot ((b\cdot a)\cdot a),a=(a\cdot (a\cdot b))\cdot (a\cdot a),a\cdot a=a\cdot (b\cdot (a\cdot a)),a=(a\cdot (a\cdot b))\cdot (a\cdot b),a\cdot a=a\cdot ((b\cdot a)\cdot b),a\cdot b=a\cdot (a\cdot (a\cdot b)),a\cdot a=a\cdot (b\cdot (a\cdot b)),a=(a\cdot a)\cdot ((b\cdot b)\cdot a),a=(a\cdot (a\cdot b))\cdot (b\cdot a),a\cdot a=((a\cdot b)\cdot b)\cdot a,a\cdot (a\cdot (a\cdot b))=b\cdot a,a\cdot a=a\cdot (b\cdot (b\cdot a)),b=((a\cdot a)\cdot a)\cdot (b\cdot b),a=(a\cdot a)\cdot ((b\cdot b)\cdot b),b=(a\cdot (a\cdot a))\cdot (b\cdot b),a=(a\cdot a)\cdot (b\cdot (b\cdot b)),b\cdot b=((a\cdot a)\cdot a)\cdot b,a\cdot a=a\cdot ((b\cdot b)\cdot b),b\cdot b=(a\cdot (a\cdot a))\cdot b,a\cdot a=a\cdot (b\cdot (b\cdot b)),(a\cdot a)\cdot a=(b\cdot b)\cdot b,b\cdot (b\cdot b)=(a\cdot a)\cdot a,a\cdot (a\cdot a)=b\cdot (b\cdot b),a=((a\cdot b)\cdot a)\cdot (a\cdot a),a=(a\cdot (b\cdot a))\cdot (a\cdot a),a\cdot a=(b\cdot (a\cdot a))\cdot a,a=((a\cdot b)\cdot a)\cdot (a\cdot b),a=(a\cdot (b\cdot a))\cdot (a\cdot b),a=(a\cdot b)\cdot (a\cdot (a\cdot b)),a\cdot b=a\cdot ((a\cdot b)\cdot a),a\cdot b=(a\cdot (a\cdot b))\cdot a,a\cdot b=a\cdot (a\cdot (b\cdot a)),a=((a\cdot b)\cdot a)\cdot (b\cdot a),a=(a\cdot b)\cdot ((a\cdot b)\cdot a),a=(a\cdot (b\cdot a))\cdot (b\cdot a),a=(a\cdot b)\cdot (a\cdot (b\cdot a)),a\cdot a=((b\cdot a)\cdot b)\cdot a,a\cdot ((a\cdot b)\cdot a)=b\cdot a,b\cdot a=(a\cdot (a\cdot b))\cdot a,a\cdot a=(b\cdot (a\cdot b))\cdot a,a\cdot (a\cdot (b\cdot a))=b\cdot a,a\cdot (a\cdot b)=(a\cdot b)\cdot a,a\cdot (a\cdot b)=a\cdot (b\cdot a),b=((a\cdot a)\cdot b)\cdot (a\cdot b),a=(a\cdot b)\cdot (a\cdot (b\cdot b)),(a\cdot a)\cdot b=(a\cdot b)\cdot b,a\cdot (a\cdot b)=a\cdot (b\cdot b),a=(a\cdot b)\cdot ((b\cdot a)\cdot a),a=(a\cdot (b\cdot b))\cdot (a\cdot a),a\cdot a=(b\cdot (b\cdot a))\cdot a,b\cdot (a\cdot a)=(a\cdot a)\cdot b,a\cdot (a\cdot b)=(b\cdot a)\cdot a,b=((a\cdot a)\cdot b)\cdot (b\cdot a),a=(a\cdot (b\cdot b))\cdot (a\cdot b),a\cdot b=((a\cdot a)\cdot b)\cdot b,a\cdot b=a\cdot (a\cdot (b\cdot b)),(a\cdot a)\cdot b=(b\cdot a)\cdot b,b\cdot (a\cdot b)=(a\cdot a)\cdot b,a=(a\cdot b)\cdot ((b\cdot b)\cdot a),a=(a\cdot (b\cdot b))\cdot (b\cdot a),b\cdot a=((a\cdot a)\cdot b)\cdot b,a\cdot (a\cdot (b\cdot b))=b\cdot a,b\cdot (b\cdot a)=(a\cdot a)\cdot b,b=((a\cdot a)\cdot b)\cdot (b\cdot b),a=((b\cdot a)\cdot a)\cdot (a\cdot a),a=((b\cdot a)\cdot a)\cdot (a\cdot b),a=(b\cdot a)\cdot (a\cdot (a\cdot b)),a\cdot b=((a\cdot b)\cdot a)\cdot a,a\cdot b=a\cdot ((b\cdot a)\cdot a),a\cdot b=(a\cdot (b\cdot a))\cdot a,a=((b\cdot a)\cdot a)\cdot (b\cdot a),a=(b\cdot a)\cdot ((a\cdot b)\cdot a),a=(b\cdot a)\cdot (a\cdot (b\cdot a)),b\cdot a=((a\cdot b)\cdot a)\cdot a,a\cdot ((b\cdot a)\cdot a)=b\cdot a,b\cdot a=(a\cdot (b\cdot a))\cdot a,a\cdot (b\cdot a)=(a\cdot b)\cdot a,b=(a\cdot b)\cdot ((a\cdot a)\cdot b),a=(b\cdot a)\cdot (a\cdot (b\cdot b)),a\cdot (b\cdot b)=(a\cdot b)\cdot a,a\cdot (b\cdot a)=a\cdot (b\cdot b),a=(b\cdot a)\cdot ((b\cdot a)\cdot a),(a\cdot b)\cdot a=(b\cdot a)\cdot a,a\cdot (b\cdot a)=(b\cdot a)\cdot a,a\cdot b=a\cdot ((b\cdot b)\cdot a),a\cdot b=(a\cdot (b\cdot b))\cdot a,(a\cdot b)\cdot a=(b\cdot b)\cdot a,a\cdot b=((a\cdot b)\cdot b)\cdot b,a\cdot b=((b\cdot a)\cdot a)\cdot a,a\cdot b=b\cdot ((a\cdot a)\cdot b),a\cdot b=(b\cdot (a\cdot a))\cdot b,a\cdot ((b\cdot b)\cdot a)=b\cdot a,a\cdot b=b\cdot ((a\cdot b)\cdot b),a\cdot b=b\cdot (b\cdot (a\cdot a)),b\cdot (a\cdot a)=(a\cdot b)\cdot b,a\cdot b=b\cdot ((b\cdot a)\cdot b),a\cdot b=b\cdot (b\cdot (a\cdot b)),(a\cdot b)\cdot b=(b\cdot a)\cdot b,a\cdot b=b\cdot (b\cdot (b\cdot a))\};$$
generateGrid[imaginaryTheorems, imaginaryAxioms, 6, 20, "Rainbow", \
True]

Note that axiom number 27, $(a\cdot b)\cdot c=a\cdot (b\cdot c)$, is a part of our axiom system (group theory). The significant factor here is that this axiom does not particularly stand out; the implication being that there is nothing special about our choice of the axiom system. Theoretically, if another axiom was chosen, and such a system was universal, it would not particularly be interesting or different. Rather, it would be plausible. The concept of computational universality implies these alternative systems are translatable to our system, but may possibly hold keys to solving problems that can be expressed, but cannot be solved with our current set of axioms.
Implications
This project was neither a mathematically sound, nor a practical exploration. Rather, the results simply point to some simple, but fundamental implications about how our mathematics is conducted. Axioms are the foundations of math, and to an arguable extent, of our universe. Therefore, the exploration of the significance, or rather the insignificance of our choice of theorems, is an important step in augmenting our view of mathematicsnot just a manipulation based on a certain system of logic, but the system of implication with a specific set of simple rules, that may differ from what we would expect.
Footnote
[1] Wolfram, Stephen. A New Kind of Science. 2018.
[2] Partially developed with code written by Jonathan Gorard, Wolfram Research
 Attachments:
Attachments: