I can't reproduce the issue, but if dragging and dropping doesn't work you should be able to click on the field to select the file from your file system browser.
With this midi file and the following settings,
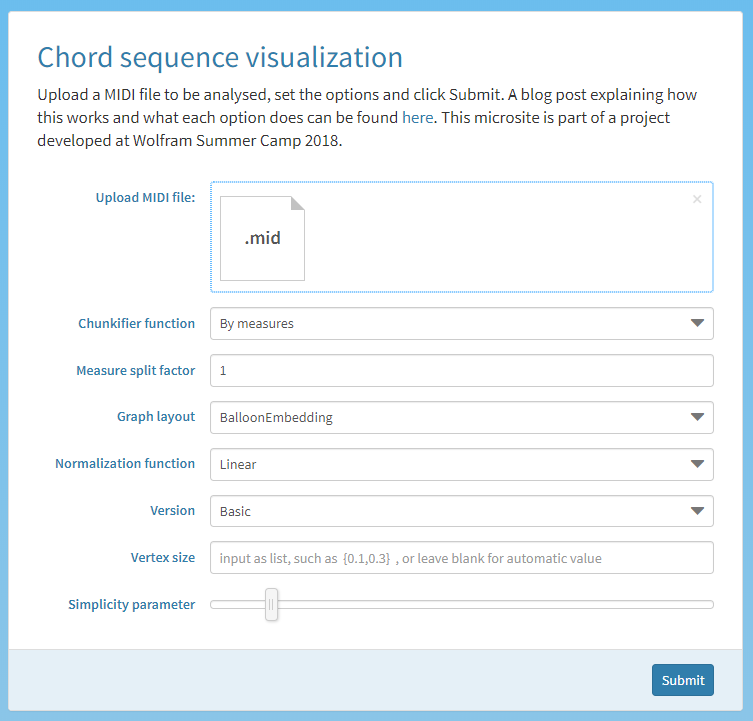
I get the following result:
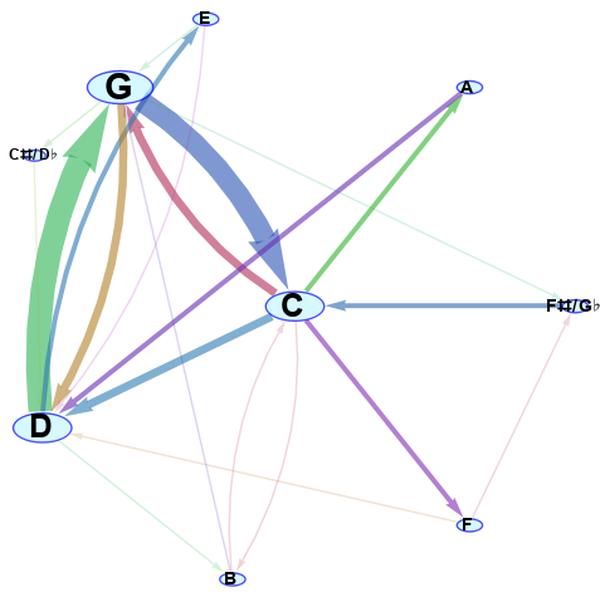
Though now that I've been playing around after a long time, I've noticed the interface is very buggy. If I ever get a license for the Wolfram Language again, I'm going to try to fix stuff :)
 Attachments:
Attachments: