I'm looking to find the frequency of a relatively large dataset (or a relatively short audio file) of a repeating sound, like so:
 Here are the original files, for those willing to play. :) eta2412 data1 Other examples: phenix140sc chaika1601
Here are the original files, for those willing to play. :) eta2412 data1 Other examples: phenix140sc chaika1601
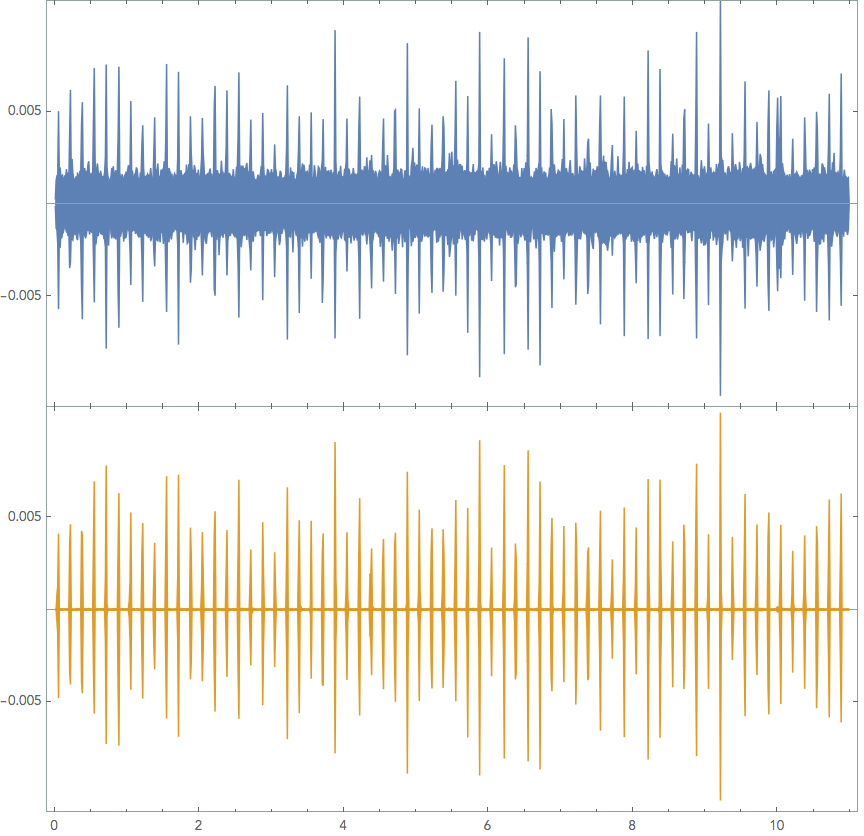
Blue is the original soundwave, and orange is a Highpass and Wiener filtered form at 44100Hz sample.
A finely zoomed in picture of each "tick" (unfiltered in an audio program) looks like so: 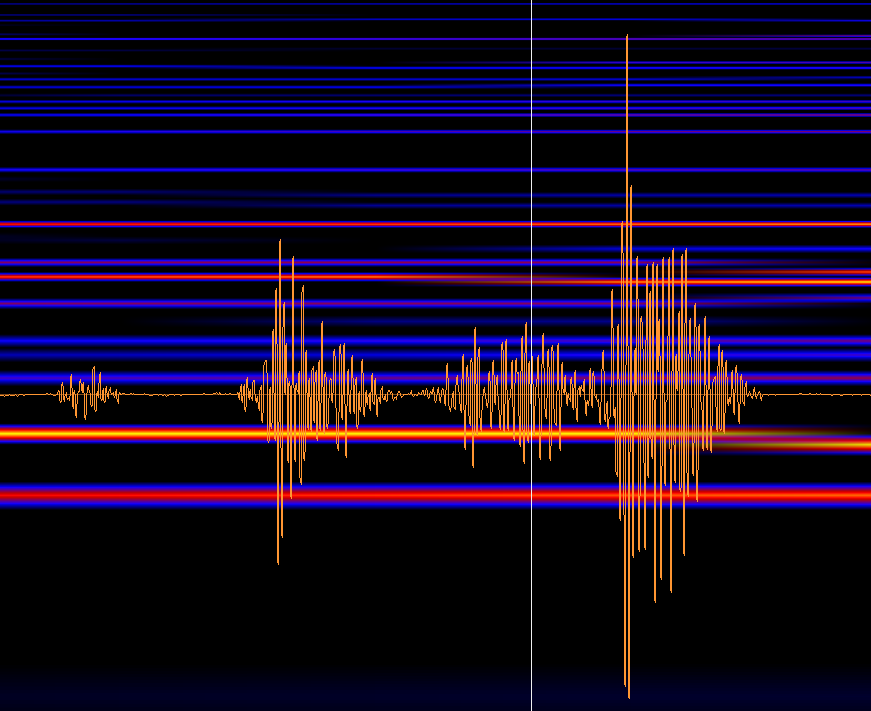
It's extremely oscillatory, however, there is a clear and obvious local maximum (when zoomed in far enough anyways (the duration of a tick is 0.016s or so)
I'm not particularly interested per say in the amplitude, however what I'd like to do, is to be able to automate and count the freq. of the "beats/ticks". This is currently done 'by hand' for each individual file I have to deal with and when a person has MMA...well, you get the point
Accuracy is a must in this case, the possible periods of the beats are at 0.200 [s] and 0.166 [s] repeating (5hz, and 6hz respectfully). Any kind of drift more than +/-0.002 second isn't acceptable.
Through many readings of this link, this link,this (the last link does nearly what but alas it's bpm) and many others, I've managed to cobble together something...that doesn't seem to get me anywhere.
dir = NotebookDirectory[];
SetDirectory[dir];
file = "eta2412.m4a";
snd = Import[file];
sndhpf = HighpassFilter[snd, 20000];
sndwf = WienerFilter[HighpassFilter[snd, 20000], 25];
sndSampleRate = Import[file, "SampleRate"];
p1 = AudioPlot[snd, PlotRange -> {{0, 5}, {-1*10^-2, 1*10^-2}}];
p2 = AudioPlot[sndwf, PlotRange -> {{0, 5}, {-1*10^-2, 1*10^-2}}, PlotStyle -> Purple];
p3 = AudioPlot[sndhpf, PlotRange -> {{0, 5}, {-1*10^-2, 1*10^-2}}, PlotStyle -> Green];
data = Flatten[AudioData[sndwf]];
data1 = Drop[data, {50000, Length[data]}];
I've attempted to do audio processing itself,
getting to
res = AudioLocalMeasurements[sndwf,"RMSAmplitude",PartitionGranularity ->{Quantity[0.1, "Milliseconds"],Quantity[0.1, "Milliseconds"]}];
ListLinePlot[res, PlotStyle -> Red, PlotRange -> {{0, 2}, {0, 0.005}}]
Show[AudioPlot[sndwf, PlotRange -> {{0, 5}, {0, 0.005}}],ListLinePlot[res, PlotStyle -> Red, PlotRange -> {{0, 5}, {0, 0.005}}], AspectRatio -> 3/6, ImageSize -> "Large"]
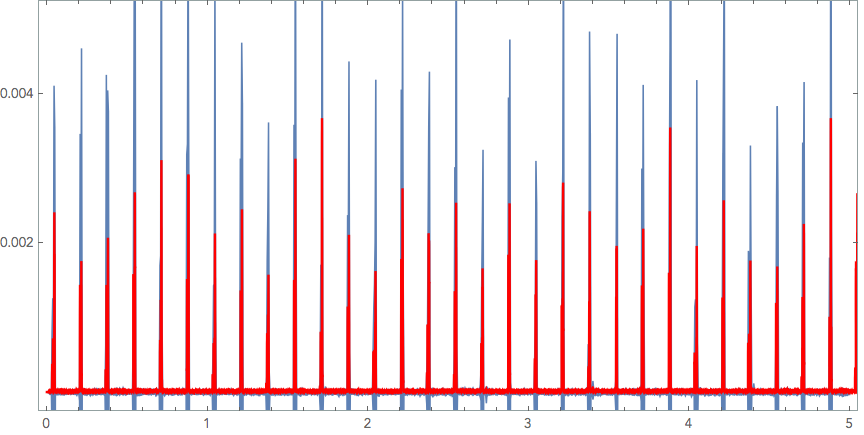
Now, I'm unfortunately at a complete loss on how to get each ticks local peak and calculate their global frequency, or rather, period.
How would one go about this? I've tried in Fourier as suggested in other posts..but the noise seems too extreme to give me anything I can understand or use to get further.
ListLinePlot[p = PeriodogramArray[data1], PlotRange -> All, ImageSize -> Large]
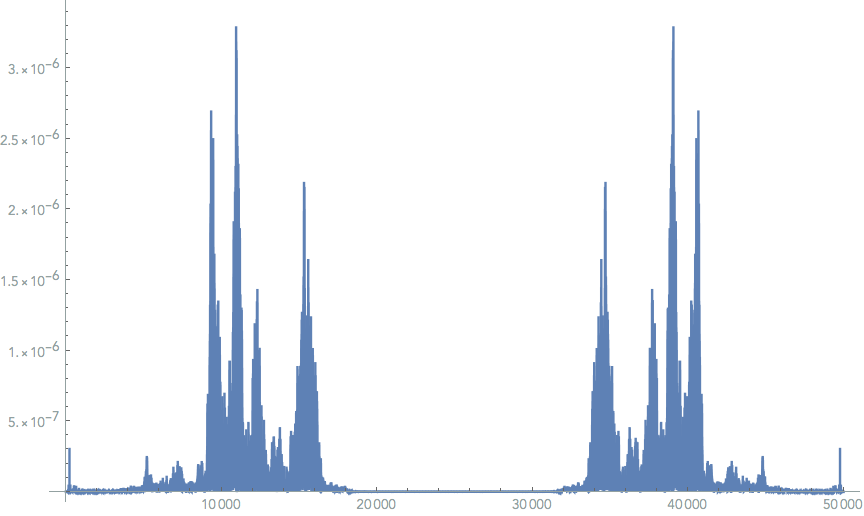
I have posted this over at stackexchange as well, incase this seems familiar to anyone. But I figured I'd try to hit two birds with two stones, should someone there post a solution I"ll gladly update it here. Thanks for the help! :)