In the example below, FindRoot doesn't work with the provided function, calcTresAtTime[mCpRes?NumericQ, mFracClr?NumericQ, timeTarget?NumericQ]. However, no problems are observed when calling the function by itself or from Plot. The documentation mentions that FindRoot first localizes all of the variables, then evaluates f with the variables being symbolic. The examples in the documentation show how to turn this off, by using ?NumericQ.
eq01ResHB =
MCpRes ures'[t] ==
mCpPump (uclr[t] - ures[t]) + UAambRes (uamb - ures[t]) +
UAbrg (ubrg - ures[t]);
eq02ClrHB =
MCpClr uclr'[t] ==
mCpPump (ures[t] - uclr[t]) + UAambClr (uamb - uclr[t]) +
UAclr (ucw - uclr[t] );
ic = {ures[0] == ures0, uclr[0] == uclr0};
eqSet = Join[{eq01ResHB, eq02ClrHB}, ic];
vars = {ures, uclr};
KuambRes = 0.025 ;
Kuabrg = 0.236;
KuambClr = 0.0024;
Kuaclr = 0.1;
calcTresAtTime[mCpRes_?NumericQ, mFracClr_?NumericQ,
timeTarget_?NumericQ] := Module[{TresSolLocal, TclrSolLocal},
parmsRes = {MCpRes -> mCpRes , UAambRes -> KuambRes,
UAbrg -> Kuabrg};
parmsClr = {MCpClr -> mFracClr mCpRes, UAambClr -> KuambClr,
UAclr -> Kuaclr};
parmsBoundary = {mCpPump -> 1, ubrg -> 200, ucw -> 60, uamb -> 70};
parmsInitialCond = {ures0 -> 70, uclr0 -> 70};
eqSetValues =
eqSet /. parmsRes /. parmsClr /. parmsBoundary /. parmsInitialCond;
{TresSolLocal, TclrSolLocal} =
NDSolveValue[eqSetValues, vars, {t, 0, 2000}];
N@TresSolLocal[timeTarget]
]
calcTresAtTime[60., 0.4, 300.]
Plot[calcTresAtTime[x, 0.4, 300.], {x, 0, 80}]
FindRoot[ 130 == calcTresAtTime[x, 0.4, 300.], {x, 0, 80}]
Below is the result of the Plot command. So this suggests that the function itself doesn't have any severe problems. 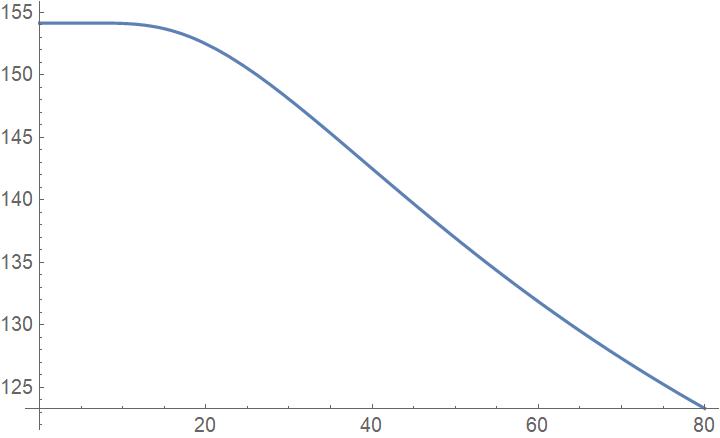
Below is the result of the FindRoot command 
Have worked through the examples in the documentation, but can't find where I have taken a wrong turn. Any help would be appreciated.
 Attachments:
Attachments: