With the NMinimize function included, the reported value is u=0.852.
That said, I tracked down the problem. To compare with my C++ results, where I use a dense sampling of (x,t) for each u in a set of 1024 and select the maximum, I used
ListLinePlot[Table[{u, h[8, u]}, {u, 0.8519, 0.8521, 0.0002/1024}]]
The output image is
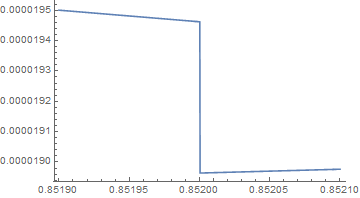
which makes it appear that there is a discontinuity at u = 0.852. The call
NMaximize[{g[8, 0.8519, x, t], 0 <= x <= 1 && 0 <= t <= 1}, {x, t}, Method -> "DifferentialEvolution"]
produces {0.0000195003, {x -> 0., t -> 0.476764}} and the call
NMaximize[{g[8, 0.8521, x, t], 0 <= x <= 1 && 0 <= t <= 1}, {x, t}, Method -> "DifferentialEvolution"]
produces {0.0000189766, {x -> 0.129624, t -> 0.521673}}. The result for u = 0.8521 is what I believe to be incorrect (and in fact incorrect for any u > 0.852 in the line-list plot). I called
Plot3D[g[8, 0.8521, x, t], {x, 0, 1}, {t, 0, 1}, PlotRange -> All, PlotPoints -> 50]
which generated the output
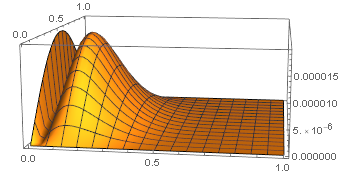
so the graph is bimodal. For u=0.8251, NMaximize reports the local maximum at (x,t)=(0.129624,0.521673). The local maximum on the boundary x=0 occurs at t=0.476541 and the value is 0.000019424, which is larger than the local maximum in the interior. I obtained the boundary computation from
NMaximize[{g[8, 0.8521, 0, t], 0 <= t <= 1}, t, Method -> "DifferentialEvolution"]