This is an example of using SmoothKernelDistribution to model stock price returns as discussed in the thread.
To download
Mathematica notebook:
CLICK HERE Get some stock data for IBM over the last 10 yearsibm = FinancialData["IBM", "FractionalChange", {2003, 11, 10}, "Value"];
ibmprice = FinancialData["IBM", {2003, 11, 10}, "Value"];
ListLinePlot[ibmprice, Filling -> Bottom, PlotRange -> All]
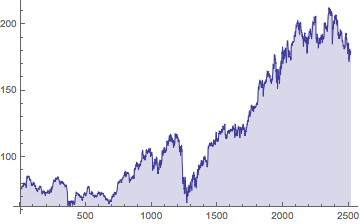
ibmfromchanges = FoldList[#1*(1 + #2) &, ibmprice[[1]], ibm];
ListLinePlot[{ibmprice, ibmfromchanges}, Filling -> Bottom, PlotRange -> All]
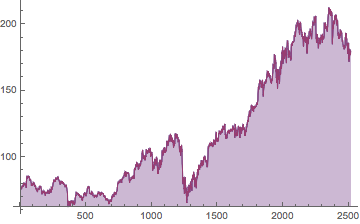
That was just to show we can use the FractionalChange property and it gives us single day returns, including dividends.
Return histogramHistogram[ibm, {.005}, "Probability"]
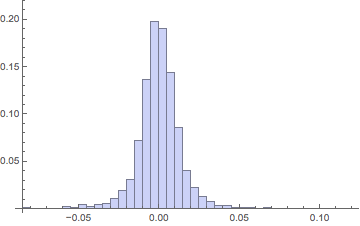
Note the high peak and long tails, with much less weight in the midrange flanks than in a normal distribution.
Basic descriptive statisticsIn[] = {Mean[#], StandardDeviation[#], Skewness[#], Kurtosis[#]} &@ibm
Out[] = {0.000428635, 0.0135803, 0.0600238, 9.54613}
Note the high figure for the Kurtosis - a Gaussian distribution would show a 3.00 on that measure.
In[] = aveannualreturn = (1 + Mean[ibm])^251 - 1
Out[] = 0.113562
we can annualize the return using 251 market days in the average year.
In[] = aveannualvolatility = (StandardDeviation[Log[1 + ibm]])*Sqrt[251.]
Out[] = 0.215138
For volatility, we annualize using the serial independence assumption, which implies the variation grows as the square root of the time. We have to use log returns to be symmetric in our treatment of proportional rises and falls.
SmoothKernel vs LogNormal ibmSKDist = SmoothKernelDistribution[Log[1 + ibm]];
In[] = E^Mean[ibmSKDist] - 1
Out[] = 0.000336473
In[] = E^Mean[ibmSKDist] - 1
Out[] = 0.000336473
ibmLNDist = LogNormalDistribution[Sequence @@ params];
In[] = Length[ibm]
Out[] = 2517
SK sampleSKsample = E^RandomVariate[ibmSKDist, 2517] - 1;
Histogram[SKsample, {.005}, "Probability"]
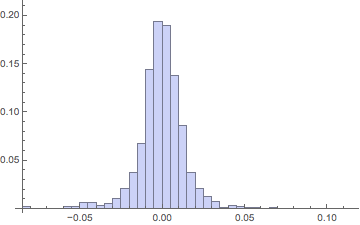
In[] = {Mean[#], StandardDeviation[#], Skewness[#], Kurtosis[#]} &@SKsample
Out[] = {-0.000258464, 0.0141158, -0.239577, 9.56601}
In[] = {Mean[#], StandardDeviation[#], Skewness[#], Kurtosis[#]} &@ibm
Out[] = {0.000428635, 0.0135803, 0.0600238, 9.54613}
Notice the excellent agreement of the smooth kernel distribution with the actual returns on Kurtosis and overall shape of the return histogram. But with only a single sample of the same length taken, the mean can easily "miss" by a significant amount.
In[] = Mean[E^RandomVariate[ibmSKDist, 2517000] - 1]
Out[] = 0.000439987
It is easy to get excellent agreement on the Mean as well by just using 1000 sample runs of the same length, rather than just one.
LN sampleLNsample = RandomVariate[ibmLNDist, 2517] - 1;
Histogram[LNsample, {.005}, "Probability"]
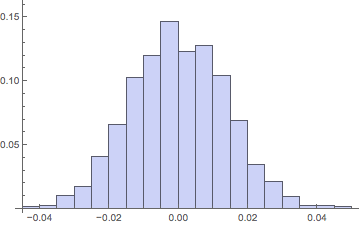
In[] = {Mean[#], StandardDeviation[#], Skewness[#], Kurtosis[#]} &@LNsample
Out[] = {0.000107968, 0.0137806, 0.057543, 2.92288}
In[] = {Mean[#], StandardDeviation[#], Skewness[#], Kurtosis[#]} &@ibm
Out[] = {0.000428635, 0.0135803, 0.0600238, 9.54613}
Notice, the lognormal distribution is able to get the first 3 moments of the distribution approximately correct, but the 4th - Kurtosis - is hopelessly low and the return histogram looks nothing like the real one as a result. It has way too much weight in the midrange flanks and not nearly enough in the small-change peak of the distribution.