Hi, i'm new to using Mathematica and i'm trying to optimize the release angle of a trebuchet using Lagrangian multipliers. I have read much about it and I have come to understand how it is calculated. I ended up going with mathematica to solve the calculations since it is quite a task by hand. I've got a trebuchet with a counterweight pendulum, and a projectile on the end of a sling: 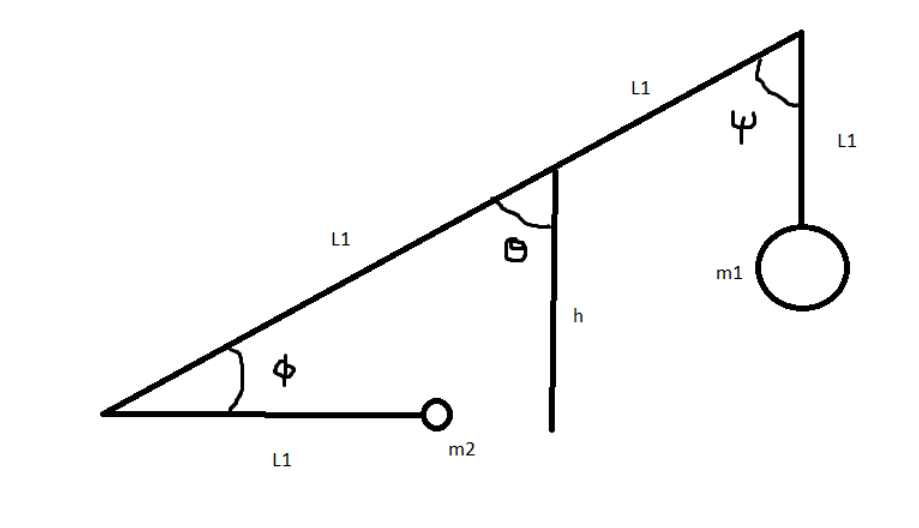
i am basing my calculations on the following info and equations https://classes.engineering.wustl.edu/2009/fall/ese251/presentations/(AAM_13)Trebuchet.pdf
I have attached my attempt in solving this using Mathematica. I have tested the method using a much simpler example with success(also attached). What I think is going wrong for me is the notation of the angular velocity and how i represent time.
I would like to find the angle(phi) and time where velocity(kinetic energy) of the projectile is the greatest with a potential energy constraint of 100.
My approach was to use L(the,phi,t)=f(the,phi)??2(g1(the,phi)?c1)-?2(g2(the,phi)?c2)
L(the,phi,t)=0
finding the gradient of 0=f(the,phi)??1(g1(the,phi)?c1)-?2(g2(the,phi)?c2)
f(the,phi)=kinetic energy being optimized, g1(the,phi)=potential energy, c1=100, g2(the,phi)=contreint for sling, c1=0
Thanks in advance
 Attachments:
Attachments: