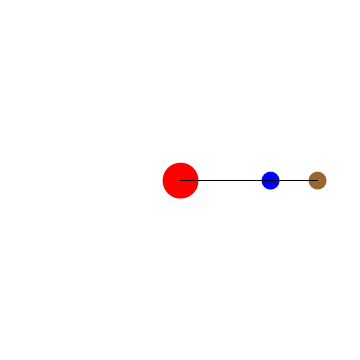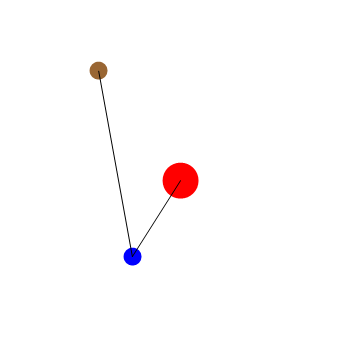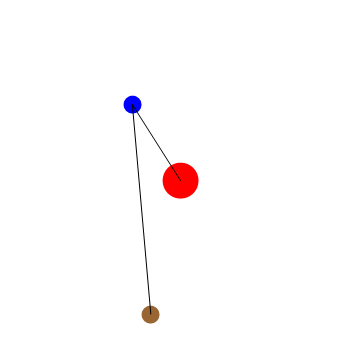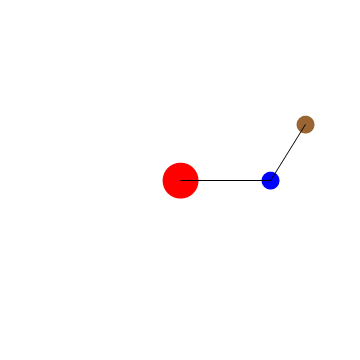
You did not put the curly braces. After the correction, we get the desired animation
G = 1; M = 1; \[Omega][r_] := Sqrt[G*M/r^3]; t0 = 4*Pi;
Animate[Graphics[{Red, Disk[{0, 0}, .2], Blue,
Disk[{Cos[\[Omega][1]*t], Sin[\[Omega][1]*t]}, .1], Brown,
Disk[{1.52*Cos[\[Omega][1.52]*t], 1.52*Sin[\[Omega][1.52]*t]}, .1],
Black, Line[{{0, 0}, {Cos[\[Omega][1]*t], Sin[\[Omega][1]*t]}}],
Line[{{Cos[\[Omega][1]*t],
Sin[\[Omega][1]*t]}, {1.52*Cos[\[Omega][1.52]*t],
1.52*Sin[\[Omega][1.52]*t]}}]},
PlotRange -> {{-2, 2}, {-2, 2}}], {t, 0, t0}]