A study on: improving the randomness of Pi
Many thanks to all those responsible for the development of Mathematica, because ALL (100.00%) numbers in this study were generated by Mathematica.
This study is the consequence of the previous reply , where I show the development of the Workbook used (Workbook 4.0 four (4) workbooks synchronized and linked, 500 points, " noise free ", 10000 digits number) and I acquired a database with 114 notorious and exotic numbers. All numbers were checked with 500 points of resolution and 10,000 digits.
Here, in this study, I collected data on the randomness generated from the interactions between Pi and another transcendental number (Champernowne type), first with Singular Interaction (20 samples), then with Compound Interaction (400 samples). With these Synthetic Random Numbers (the ones that were built for the sole purpose to have the best random performance) I expected to get interesting results regarding the behavior of how random varies after interactions between the two target transcendental numbers.
(Objectives):
Find a number with the performance of randomness greater than all other numbers.
Test which type of interaction is the best to be done between two transcendental numbers to increase randomness in the result. In this study I compared Sum and Product interactions.
(Method):
The transcendental number I chose to interact with Pi was the transcendental number series: ChampernowneNumbers(x), since this particular series had good results for randomness and because we can vary the X to have more samples in the result. In this study I used the X from 2 to 11.
I do this study in two ways: Singular Interaction (20 samples) and Compound Interaction (400 samples).
(Singular Interaction):
The Singular Interaction is of the type:
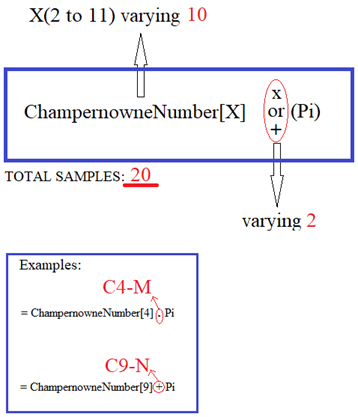
This is the following result:
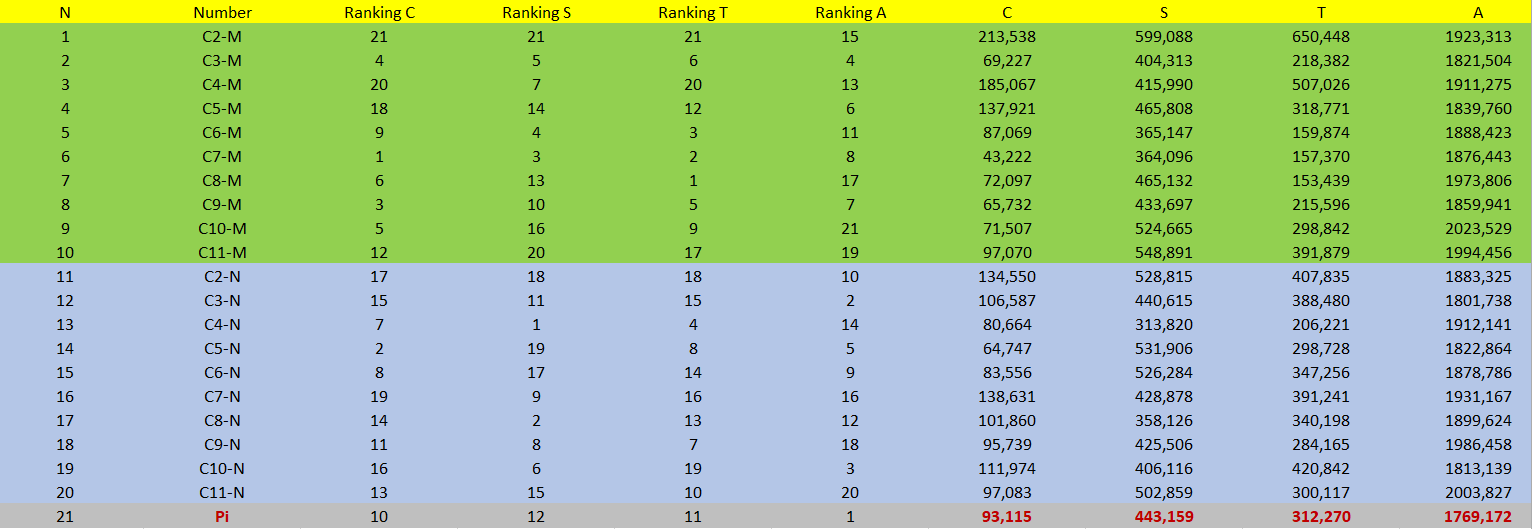
The following charts (20 Singular Interaction) to get an idea of the data acquired:

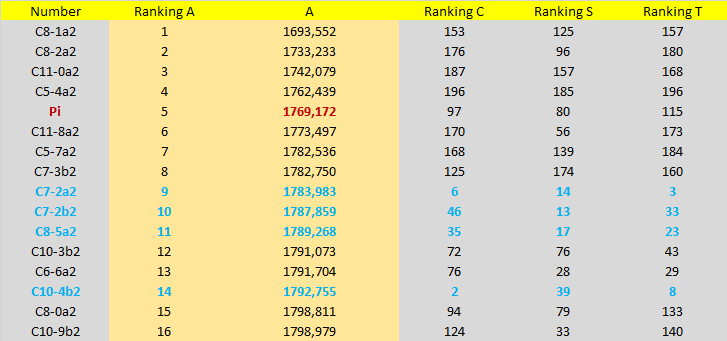
Now the best ranking of the characteristic A in Singular Interaction:
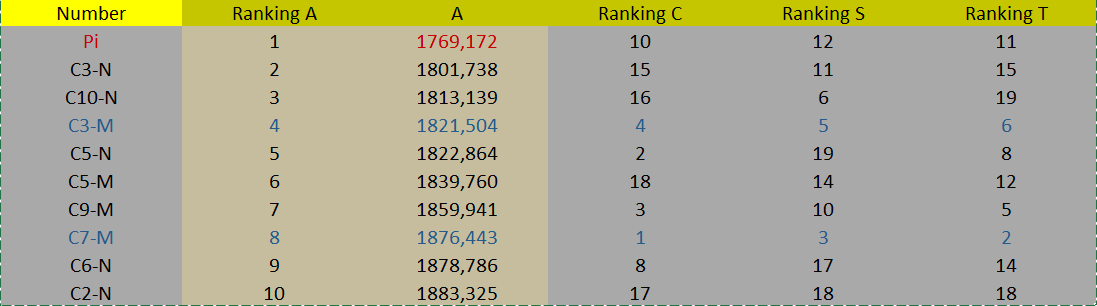
(Partial Conclusion):
Use: 20 samples. None of the numbers in this Singular Interaction performed better than the performance of Pi on all attributes. No number had the characteristic A smaller than that of Pi. Only two candidates obtained good and balanced performances despite characteristic A more than Pi: C3-M and C7-M. It was not possible to see differences between Sum and Product operations between these two transcendental numbers because there was little sampling in this Singular Interaction.
In the next type of interaction below we will explore more systematically the operations (Compound Interaction).
(Compound Interaction):
The Compound Interaction is of the type:
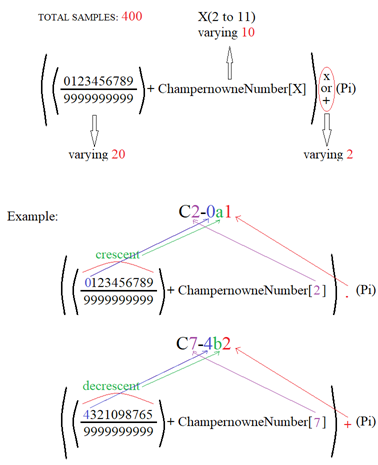
The first term is the shifting number and varying as:

In this type of interaction the result was systematically explored among 400 sample numbers. 200 with Sum operation and 200 with Product operation. The result is as follows.
These are the numbers tested (just so we can get an idea of the data):

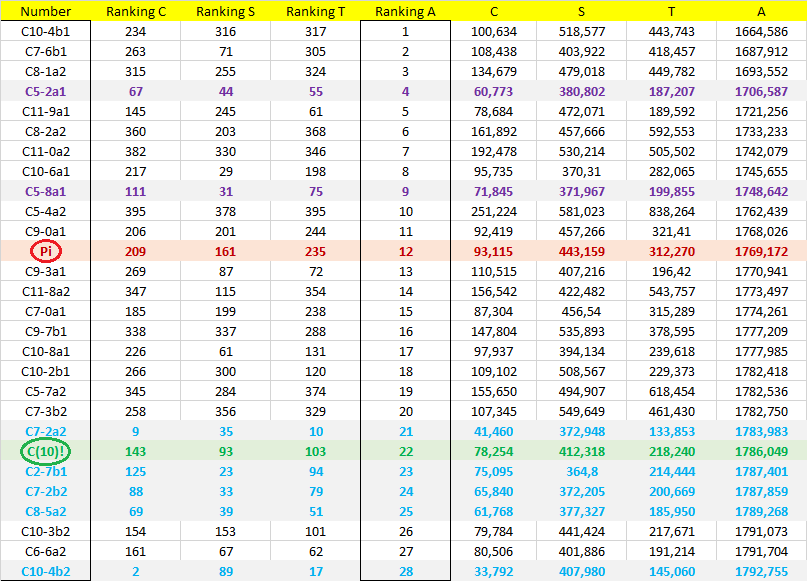
Partial result table of Product interaction with Pi:

Partial result table of Sum interaction with Pi:
Analysis of the numbers found, Sum and Product, comparing with Pi and ChampernowneNumber(10)! (which was the previous star):
(Conclusion):
Best Synthetic Random Numbers I get:
I can classify the result of the best random numbers found as follows:
C(10)! type efficiency (light blue in chart above): Candidates similar or better than ChampernowneNumber(10)! performance (the previous "star"), there are 5: 1 found by Product and 4 found by Sum. The numbers: C7-2a2, C2-7b1, C7-2b2, C8-5a2 and C10-4b2. They are very good candidates, like C(10)!
Super-Candidates type efficiency (purple in chart above): Candidates that exhibit super-efficiency of randomness. There are only 2, found by Product. The super-candidates are:
C5-8a1 (second best)
C5-2a1 (best of ALL)
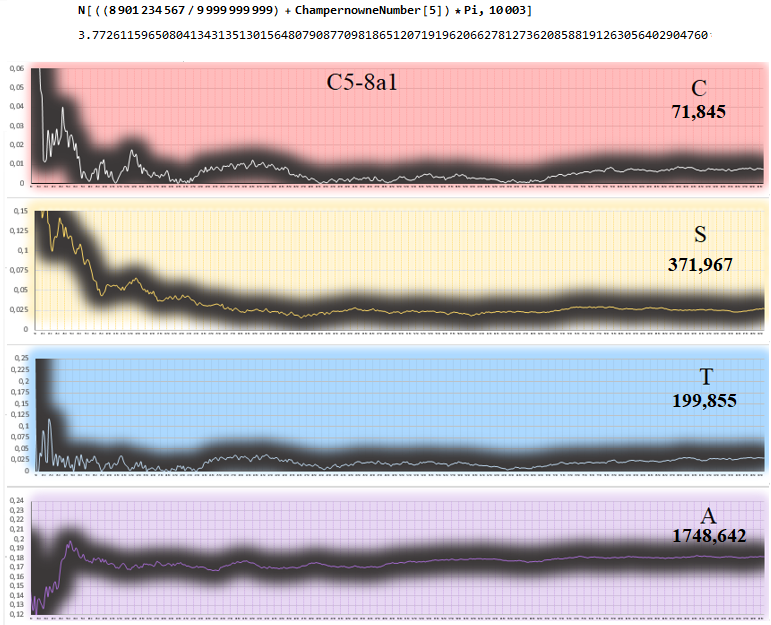
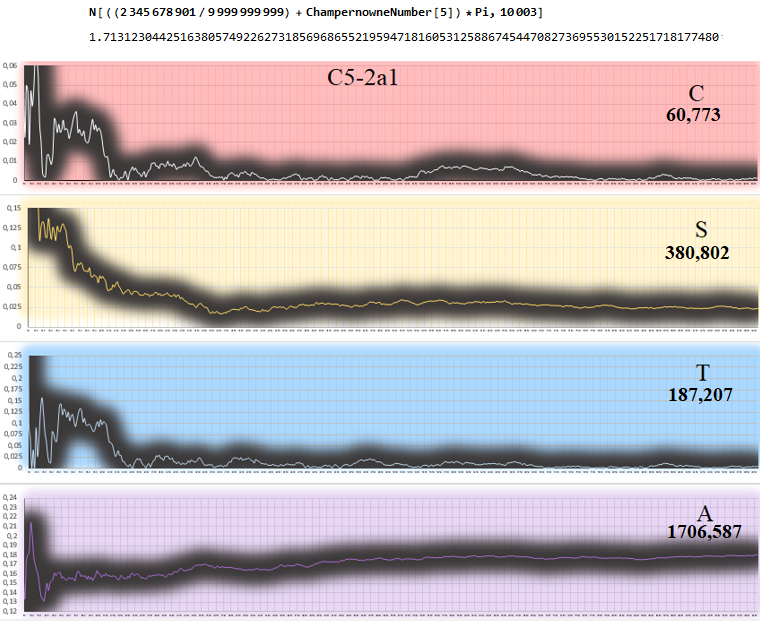
This number C5-2a1 is the best number among the 534 numbers of my database joining the two posts: among which many of them are Notorious, Exotic, Champernowne Series and Synthetic Random Numbers.
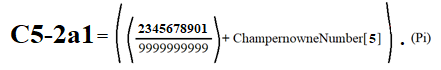
Three numbers: C8-1a2, C7-6b1 and C10-4b1 surpassed E^(1/Pi) in characteristic "A" ! But they are not very balanced in other features.
Finally, a concrete result was found to improve Pi's randomness in these two super candidates!
The use of this Synthetic Random Number super-candidate ranges from simulations to dice apps and random number generators.
Best Operation:
Exact 100 Compound Interaction numbers are better than Pi in C, S and T simultaneously, 52 by Product and 48 by Sum, another 300 are worse than Pi. Although only 11 numbers found have the characteristic A better than Pi, Pi has median characteristics C,S,T in comparison to this type of number analysed.

We can conclude that it is INCONCLUSIVE what kind of operation is best to increase randomness by interacting two transcendental numbers, since both Sum and Product gave results without any tendency or visible improvement, only average non-favorable results and some optimal peaks as expected. This is interesting to me particularly since I thought that Sum would give better results by adding a well-distributed rational part of digits to the target numbers. But both ways gave similar results. Even with these 400 samples it remains inconclusive whether it is better to improve randomness with Sum or Product interactions.
This study took 11 days (4 hours a day) to be performed.
Attached is the full table of the 534 numbers.
 Attachments:
Attachments: