Message Boards Message Boards

0
|
4310 Views
|
4 Replies
|
2 Total Likes
View groups...
Share
Share this post:

Are results exact, or a really good approximation?

Mohamed Salem
Posted 11 years ago
I have no idea where to post this question!! Here it goes:  If my input is: '((2^756,839)-1) * ((2^1,257,787)-1)' ; Will the result be an excellent approximation(near exact) or the exact answer? 
POSTED BY: Mohamed Salem
4 Replies
Sort By:
This sort of question can be sent directly to the Wolfram|Alpha folks by entering it in the "Give us your feedback"
window at the bottom of the page.  (The little slot opens wide when you start typing into it.)
POSTED BY: Bruce Miller
Thank you, Szabolcs.

With Wolfram|Alpha, the output for  ((2^756,839)-1) * ((2^1,257,787)-1)   says it is a "Decimal approximation".
If you keep pressing the "More Digits" button you will eventually reach excellent approximation, then (maybe)
exact.



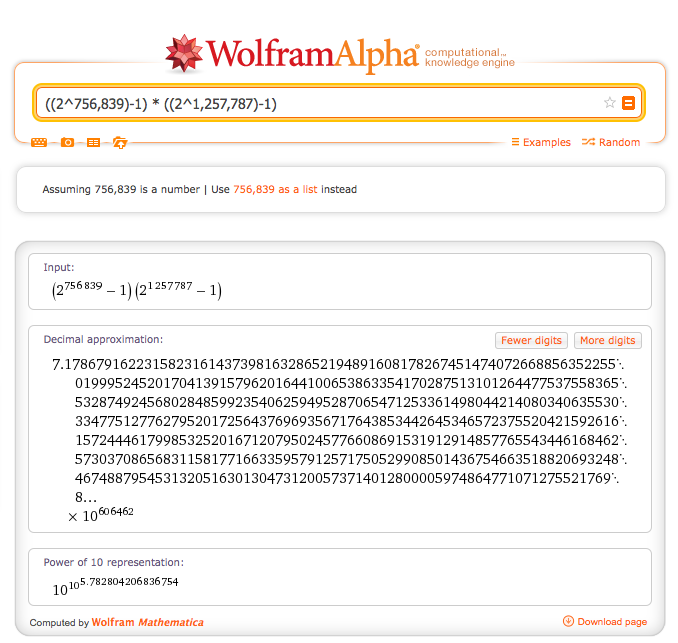
When I gave Wolfram|Alpha the input 
        ((2^756,839)-1) * ((2^1,257,787)-1)   exact 
it ran out of time doing the calculation and returned nothing.
POSTED BY: Bruce Miller
 Mohamed, you should probably make it clear that your question refers to Wolfram|Alpha and not  Mathematica, otherwise people will misunderstand it (like Bruce did).

(The original question, deemed off topic for Mathematica.SE,  was here.)
POSTED BY: Szabolcs Horvát
The usual rule is exact in, exact out.  Some numerical functions convert exact inputs to the specified approximation.

(fyi, omit the commas.)
In[8]:= ((2^756839)-1) * ((2^1257787)-1)   // Short                                     

Out[8]//Short= 717867916223158231614373981632865219489160<<606398>>95739805181539094888449

<<606398>>  means   606398  digits were omitted.  The output is very long.

A good starting place is http://reference.wolfram.com/mathematica/tutorial/ExactAndApproximateResults.html.
POSTED BY: Bruce Miller
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract