I will show the working code and the solution to task 2
t0 = 9; P = 14; lr = 1; g = 9.8; m = 1; ks = 100; kd = 10;
eqns = {Table[
m*x[i]''[t] == -ks*(Sqrt[(x[i][t] - x[i - 1][t])^2 + (y[i][t] -
y[i - 1][t])^2] - lr)*(x[i][t] - x[i - 1][t])/
Sqrt[(x[i][t] - x[i - 1][t])^2 + (y[i][t] - y[i - 1][t])^2] -
ks*(Sqrt[(x[i][t] - x[i + 1][t])^2 + (y[i][t] -
y[i + 1][t])^2] - lr)*(x[i][t] - x[i + 1][t])/
Sqrt[(x[i][t] - x[i + 1][t])^2 + (y[i][t] - y[i + 1][t])^2] -
kd*(x[i]'[t] - x[i - 1]'[t]) - kd*(x[i]'[t] - x[i + 1]'[t]), {i,
2, P - 1}],
Table[m*y[i]''[
t] == -ks*(Sqrt[(x[i][t] - x[i - 1][t])^2 + (y[i][t] -
y[i - 1][t])^2] - lr)*(y[i][t] - y[i - 1][t])/
Sqrt[(x[i][t] - x[i - 1][t])^2 + (y[i][t] - y[i - 1][t])^2] -
ks*(Sqrt[(x[i][t] - x[i + 1][t])^2 + (y[i][t] -
y[i + 1][t])^2] - lr)*(y[i][t] - y[i + 1][t])/
Sqrt[(x[i][t] - x[i + 1][t])^2 + (y[i][t] - y[i + 1][t])^2] -
kd*(y[i]'[t] - y[i - 1]'[t]) - kd*(y[i]'[t] - y[i + 1]'[t]) -
m*g, {i, 2, P - 1}]};
ic = {Table[y[i]'[0] == 0, {i, 1, P}], Table[y[i][0] == 0, {i, 1, P}],
Table[x[i][0] == lr*(i - 1), {i, 1, P}],
Table[x[i]'[0] == 0, {i, 1, P}]};
bc = {x[P]''[t] == 0 , x[1]''[t] == 0, y[P]''[t] == 0, y[1]''[t] == 0};
Y = NDSolveValue[{eqns, ic, bc},
Table[y[i][t], {i, 1, P}], {t, 0, t0}]; X =
NDSolveValue[{eqns, ic, bc}, Table[x[i][t], {i, 1, P}], {t, 0, t0}];
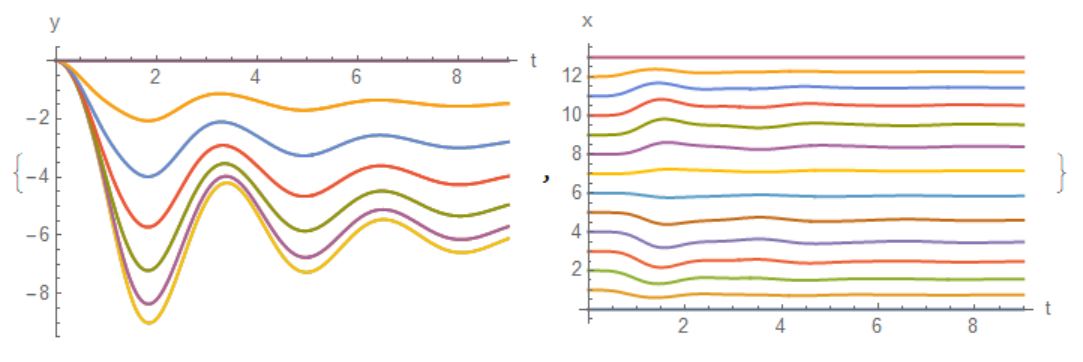
{Plot[Y, {t, 0, t0}, PlotRange -> All, AxesLabel -> {"t", "y"}],
Plot[X, {t, 0, t0}, PlotRange -> All, AxesLabel -> {"t", "x"}]}
This figure shows the coordinates of the point masses.
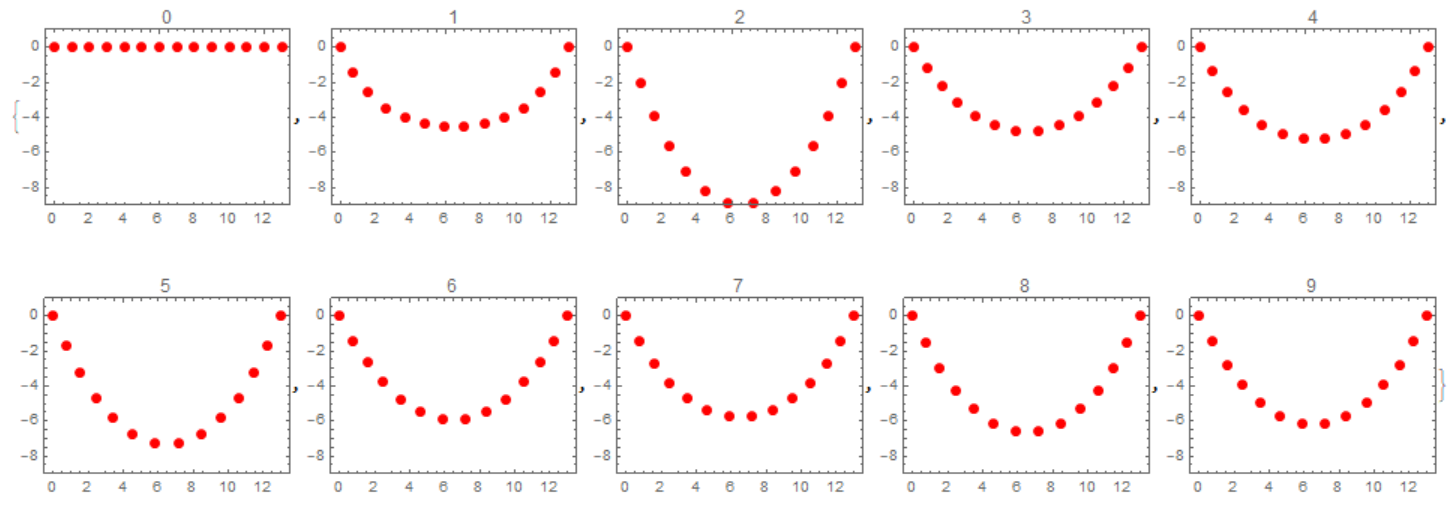
 These coordinates can be displayed on the plane.
These coordinates can be displayed on the plane.
Table[Graphics[{PointSize[Large], Red,
Point[NDSolveValue[{eqns, ic, bc},
Table[{x[i][tn], y[i][tn]}, {i, 1, P}], {t, 0, tn}]]},
Frame -> True, PlotLabel -> tn,
PlotRange -> {{-.5, 13.5}, {-9, 1}}], {tn, 0, t0, 1}]
Velocity components of point masses
VY = NDSolveValue[{eqns, ic, bc},
Table[y[i]'[t], {i, 1, P}], {t, 0, t0}]; VX =
NDSolveValue[{eqns, ic, bc}, Table[x[i]'[t], {i, 1, P}], {t, 0, t0}];
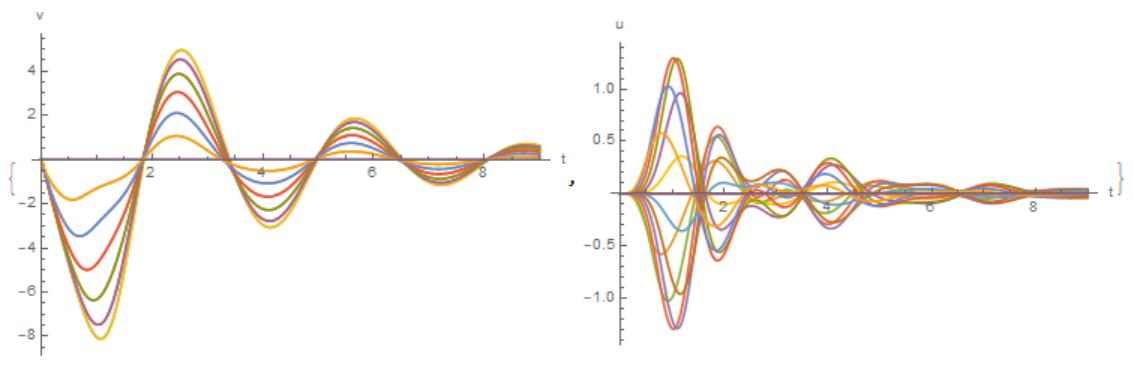
{Plot[VY, {t, 0, t0}, PlotRange -> All, AxesLabel -> {"t", "v"}],
Plot[VX, {t, 0, t0}, PlotRange -> All, AxesLabel -> {"t", "u"}]}