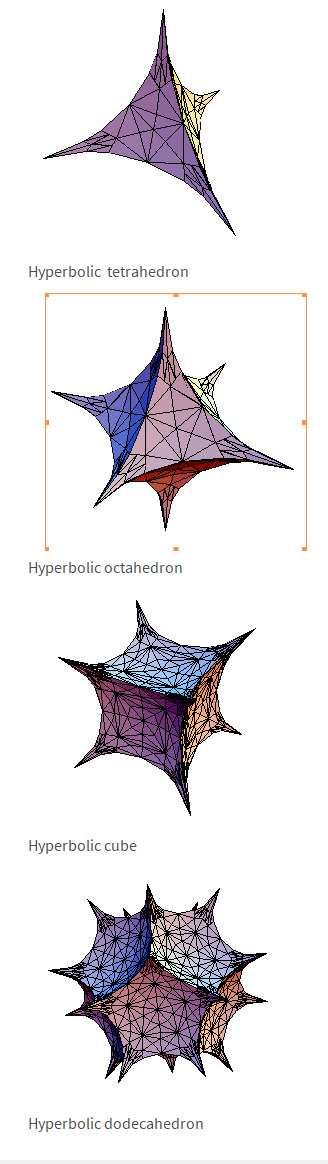
Yes I saw that while I was looking for the equations. It could be that I'm not using the software correctly, but all I see is this (image shown at the bottom of this reply). After examining the source code, it seems like all it does is plot hardcoded lines and does not use a specific equation.
I also discovered this from my searching, but unfortunately this is also a dead end. The code simply loads a platonic solid and applies a hyperbolic map on it ( ).
).
From the above demo, I realized that the equations I have for the Hyperbolic Octahedron do not exactly mimic what is happening in the demo. For instance, the implicit equation is:
0 = x^(2/3) + y^(2/3) + z^(2/3) + r^(2/3)
Changing the exponents between 0 and 1 would "hyperbolize" the octahedron as shown in the above demo, but as the exponent tends to infinity the surface approximates a square, unlike the above demo where bulbs are formed.