In the United States from the late 1960s to the early 1970s there was a fad for making string art. In basement workshops and garages all over the country, amateur artists whiled away their free time stringing colorful bits of yarn between little tacks hammered into felt-covered plywood. The resulting artwork looked vaguely mathematical, and I recall that a photograph of one such piece graced the cover of my seventh grade mathematics textbook.
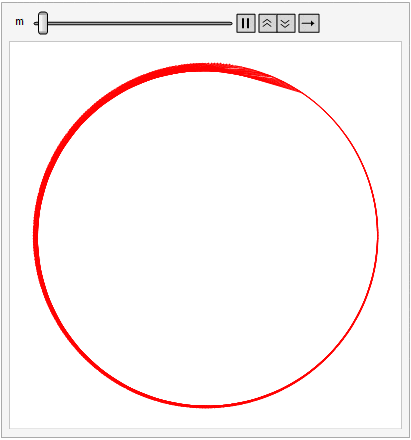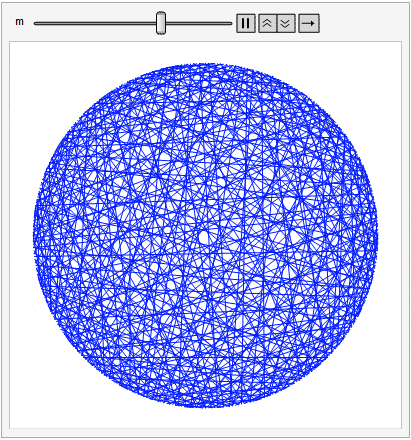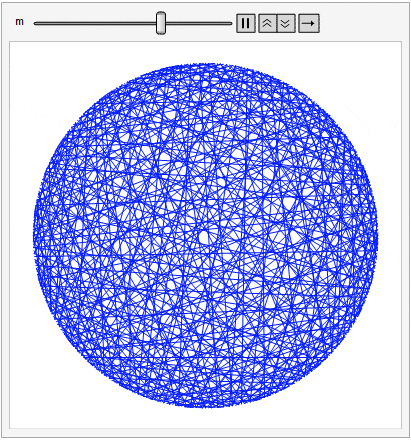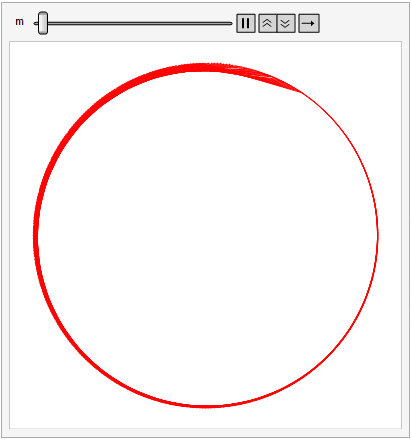
For this post, imagine 360 tacks spaced evenly around a circle. Beginning at the top (i.e., the 12:00 position) label the tacks from 0 to 359 proceeding clockwise. Choose a constant m. Then, for points i = 0 to 359, draw a line (or string a piece of yarn if you wish) between tack i and tack (i m) mod 360.
Different values of m produce different patterns, but allowing m to vary smoothly between 1 and 360 produces a psychedelic effect that might have inspired Dr. Timothy Leary back in the day.
The Mathematica code is very simple:
base = 360;
max = 359;
plist = {Sin[(2.*Pi*#/base)], Cos[2.*Pi*#/base]} & /@
Range[0, base - 1];
colors = Table[Hue[x], {x, 0, 1, 1./base}];
zlist[p_, m_] :=
Table[{p[[i + 1]], p[[Mod[IntegerPart[m*i], base] + 1]]}, {i,
base - 1}]
stringArt =
Animate[Graphics[{colors[[IntegerPart[m]]],
Line[zlist[plist, m]]}], {m, 1.1, base - 0.1, 0.1},
AnimationRate -> 3, AnimationRunning -> True,
AnimationDirection -> Forward, AnimationRate -> .1]
The gif doesn't really do it justice; to get the full effect I suggest you run the code in your own copy of Mathematica.