One year ago

One year ago I posted my first publication about implementation the topology optimization algorithms in Wolfram Mathematica by using my own finite element method. I want to continue this post by presenting new results, which I received during year.

Introduction

It is really important problem in aircraft and spacecraft engineering. Why? Because the main goal of using topology optimization algorithms in such spheres is a decreasing the weight of any construction. As example - full optimization of the aircraft wing: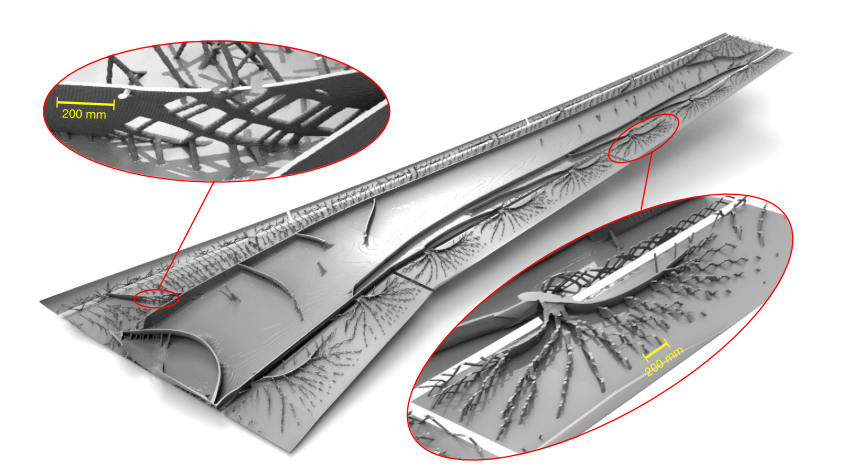 Results of this optimization presented by Niels Aage, Erik Andreassen, Boyan S. Lazarov and Ole Sigmund in their paper ["Giga-voxel computational morphogenesis for structural design"][3]. They achieived the 20-40% saving of weight with saving the durability with using SIMP (Solid Isotropical Material with Penalization) method. It is incredible result because of it is the first paper about optimizing object of such scale. It is important to say that now it is not fantastic idea to optimize multiscale objects or object with huge amount of components. Many commercial products realized their own algorithms.

What did I do?

• SIMP 2D algorithm (not my own)
• SIMP 2D modification (my own realization by FindMinumum function, but not effective in comparison with traditional algorithm, but I can use any type of elements)
• SIMP 3D algoritm (not my own)
• Level-set 2D algorithm (not my own)
• Level-set 3D algorithm based on 2D (my own)
• Modifications in methods for better quality of solutions (my own)

SIMP 3D algorithm in Matlab was written by Kai Liu and Andres Tovar in paper "An efficient 3D topology optimization code written in MATLAB". It should be mentioned that Ole Sigmund and Martin Philip Bendsoe were first men who published effective numerical algorithm of first topology optimization algorithms.

Level-set 2D algorithm was written by Vivien J. Challis in paper "A discrete level-set topology optimization code written in MATLAB".

It was a little sad that most of realizations of topology optimization algorithm were written in MATLAB. I found only one implementation of SIMP method in Wolfram Mathematica written by Vladimir Uskov.

SIMP

So I realized these algorithms in Wolfram Mathematica. Both of them have a simple implementation of FEM. In 2D case we have quad elements with first order interpolation, and in 3D case - hexahedron elements with first order interpolation. It should be mentioned that also I realized not effective topology optimization algorithm based on Wolfram Mathematica function FindMinimum and NDSolve`FEM` module in Mathematica. This function has a solver for constrained optimization problem based on Interior point method of Narendra Karmarkar. Here some solutions of traditional topology optimization problem I received by using this function:

Graphical formulation of topology optimization problem.

First order element with first order penalty function

Second order element with first order penalty function

Second order element with second order penalty function

Second order quad element with second order penalty function

All results and code you can look on my GitHub page in file TopOpt2.nb.

SIMP 3D implementation results you can look below:

Algorithm realization you can look also on my GitHub page in file SIMP3D.nb.

Level-set

I translated the educational code of Vivien J. Challis from MATLAB code to Wolfram Mathematica with saving the names of variables for better understanding by my readers. You can look all meanings of all variables in his publication "A discrete level-set topology optimization code written in MATLAB". I decided that it will be good to make an animation for any future user of level-set topology optimization for clear understanding of the idea:

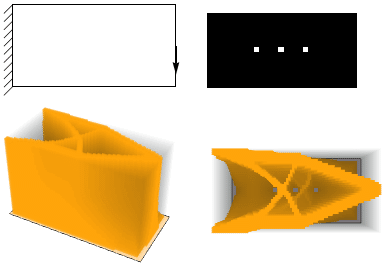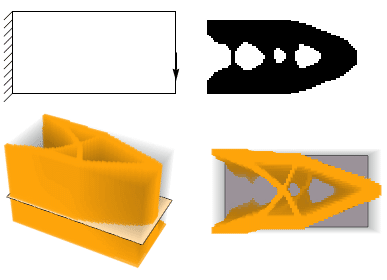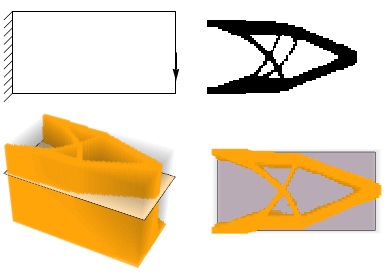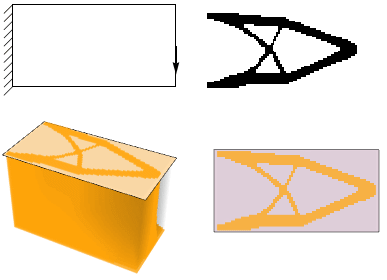
Here we can see the how we receive the solution of problem by level-set algorithm. It is interesing that the same method is used for receiving 3D model from Magnetic resonance imaging. Hamilton-Jacobi equation and volume constraints, which describe our optimization problem define by itself 3D surface in 2D case problem. In 3D problem it will be 4D surface. And algorithm only move the plane through this surface until it receives the correct solution. Below 3D case is presented:

Here you can see the possible solution of 3D case problem. But the main difference between SIMP and Level-set is a possibility to modify internal domain. Without topology sensitivites in 2D and 3D level-set method - internal domain modification forbidded. We can make an initial hole inside the body for overwhelming this forbid. FEM implementation of voxel mesh was taken from paper Kai Liu and Andres Tovar. Idea of realization 3D Level-set was taken from paper Vivien J. Challis. In my research I tried to change the algorithm of satisfying constrained optimization from Lagrange multiplier method to something heuristic algorithm. The main Idea was avoiding of seeking right values of Lagrange multipliers. Standard and modificated algorithms were realized and compared. I received the longer convergence of algorithm, but I need only 1 run for any optimization problem. Standard and modificated realization and comparison you also can look on GitHub page in file Level-set3D.nb.

Further Exploration

Now is appeared a new implementation of Level-set algorithm based on reaction-diffusion equation. The main advantage of this is an independence level-set function on nucleation process. Possibly all implementations will be united in mini-extension of Wolfram Mathematica.

Acknowledgements

I want to thank Dr. Vivien Challis from The University of Queensland for clear explanations and helpful conversation about 3D Level-set method implementation.