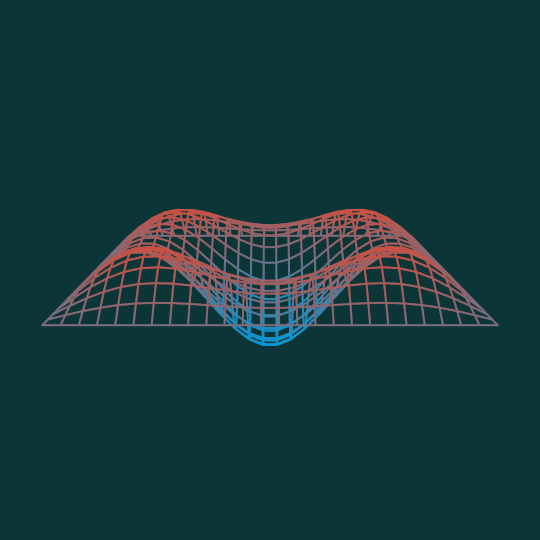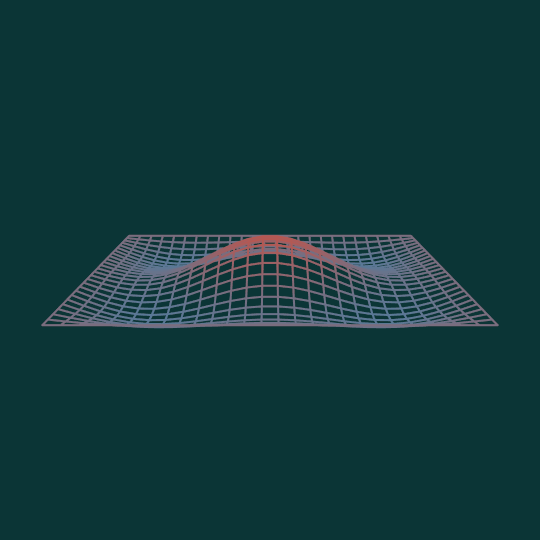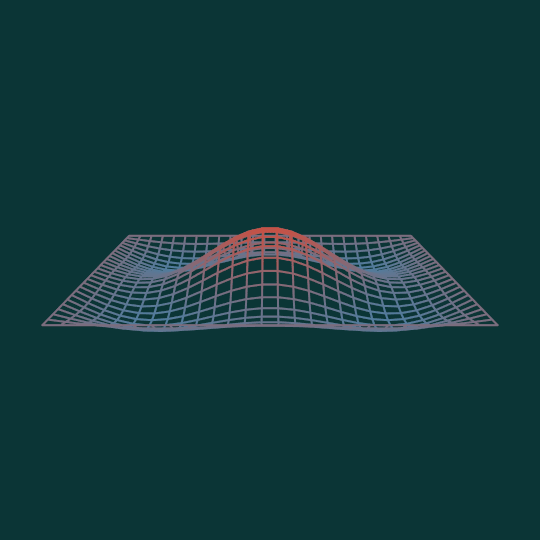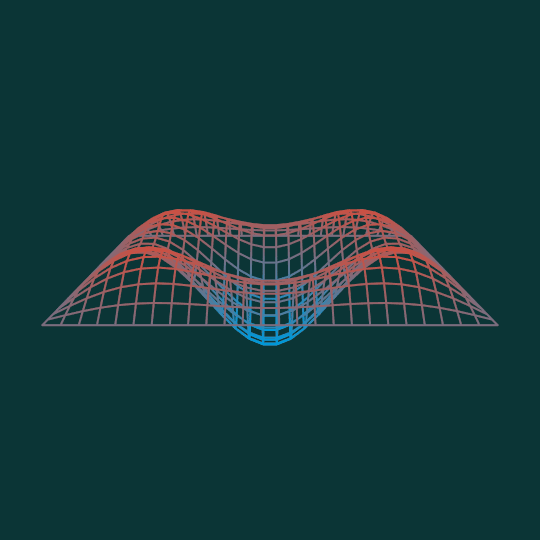
Bounce
The vibration modes of a rectangular membrane of width $L_x$ and length $L_y$ are
$\Psi_{mn}(x,y) = \sin\left(\frac{\pi m}{L_x}x\right) \sin\left(\frac{\pi n}{L_y}y\right);$
in other words, each direction just consists of standing waves with wavelength given by the reciprocal of some integer multiple of the length of the side of the membrane.
?[m_, n_, {x_, y_}] := Sin[m ? x] Sin[n ? y];
In general these modes all have different frequencies, but when, e.g., one side length is a multiple of the other, it is possible for two different modes to have the same frequency, and then linear combinations of modes of the same frequency will also be vibration modes of the membrane. See Dan Russell's demo for more.
This animation shows the combination of the $(1,3)$ mode and the $(3,1)$ mode of the square where each factor is equally weighted. (Compare previous vibration mode animations Square Up, Drumbeat, and Things That Go Bump in the Night).
Here's the code:
DynamicModule[{n = 25, a = 1.2, dots,
cols = RGBColor /@ {"#0098d8", "#f54123", "#0b3536"}},
Manipulate[
dots = Table[
{2 ? (x - 1)/n, 2 ? (y - 1)/n,
Cos[?] (1/Sqrt[2] ?[3, 1, {(x - 1)/n, (y - 1)/n}] + 1/Sqrt[2] ?[1, 3, {(x - 1)/n, (y - 1)/n}])},
{x, 1, n + 1}, {y, 1, n + 1}];
Graphics3D[
{AbsoluteThickness[2],
Table[
Line[#[[i]], VertexColors -> (Blend[cols[[;; -2]], (# + a)/(2 a)] & /@ #[[i, ;; , 3]])],
{i, Length[#]}] & /@ {dots, Transpose[dots]}},
Boxed -> False, PlotRange -> {{0, 2 ?}, {0, 2 ?}, {-2, 2}},
ImageSize -> 540, ViewPoint -> {2, 0, 1/2},
SphericalRegion -> True, Background -> cols[[-1]]],
{?, 0, 2 ?}]
]