Message Boards

WOLFRAM COMMUNITY

13223 Views

4 Replies

6 Total Likes

View groups...

Follow this post

Share this post:

GROUPS:

Staff Picks Mathematics Visual Arts Dynamic Interactivity Geometry Graphics and Visualization Wolfram Language

[GIF] Bounce ((3,1)+(1,3) vibration mode of a square membrane)

Clayton Shonkwiler

Clayton Shonkwiler, Colorado State University

Posted 6 years ago

Bounce The vibration modes of a rectangular membrane of width $L_x$ and length $L_y$ are $\Psi_{mn}(x,y) = \sin\left(\frac{\pi m}{L_x}x\right) \sin\left(\frac{\pi n}{L_y}y\right);$ in other words, each direction just consists of standing waves with wavelength given by the reciprocal of some integer multiple of the length of the side of the membrane. ?[m_, n_, {x_, y_}] := Sin[m ? x] Sin[n ? y]; In general these modes all have different frequencies, but when, e.g., one side length is a multiple of the other, it is possible for two different modes to have the same frequency, and then linear combinations of modes of the same frequency will also be vibration modes of the membrane. See Dan Russell's demo for more. 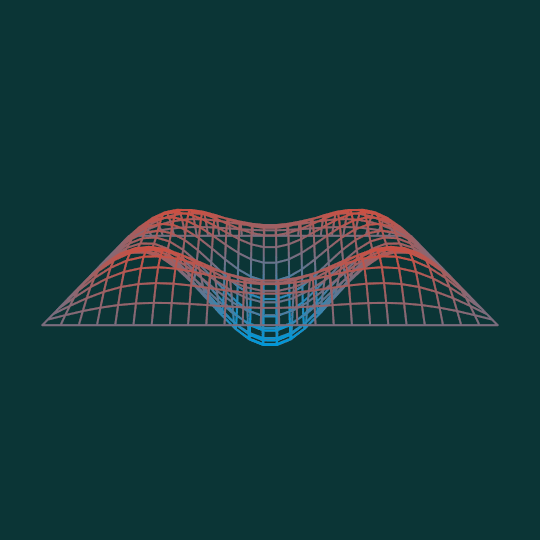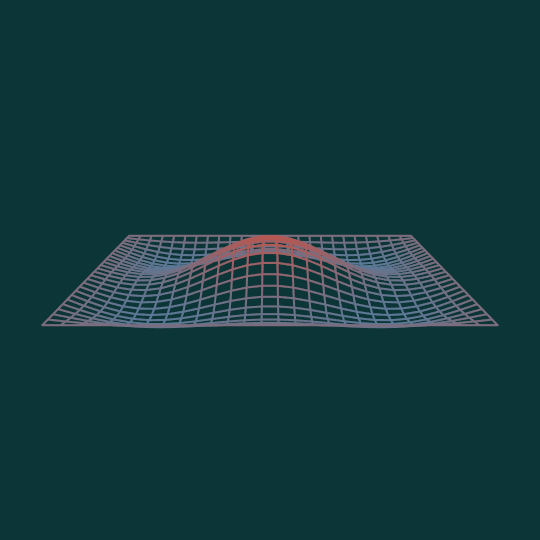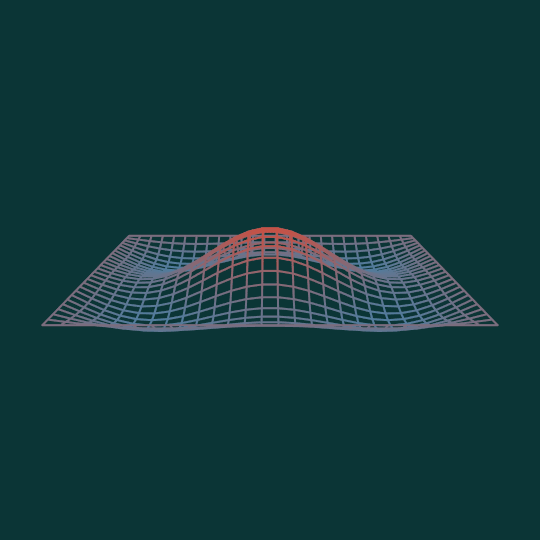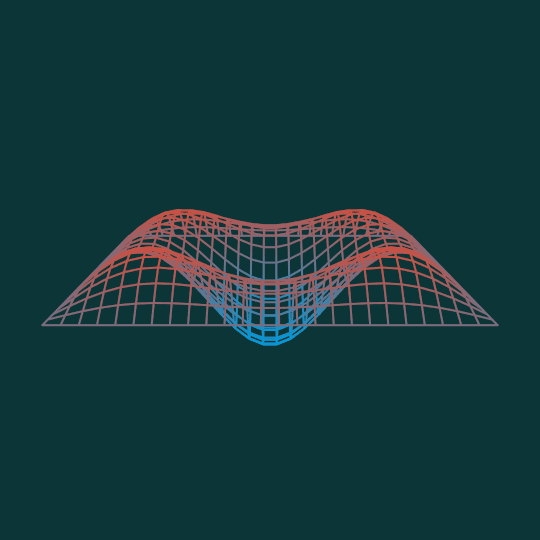This animation shows the combination of the $(1,3)$ mode and the $(3,1)$ mode of the square where each factor is equally weighted. (Compare previous vibration mode animations Square Up, Drumbeat, and Things That Go Bump in the Night). Here's the code: DynamicModule[{n = 25, a = 1.2, dots, cols = RGBColor /@ {"#0098d8", "#f54123", "#0b3536"}}, Manipulate[ dots = Table[ {2 ? (x - 1)/n, 2 ? (y - 1)/n, Cos[?] (1/Sqrt[2] ?[3, 1, {(x - 1)/n, (y - 1)/n}] + 1/Sqrt[2] ?[1, 3, {(x - 1)/n, (y - 1)/n}])}, {x, 1, n + 1}, {y, 1, n + 1}]; Graphics3D[ {AbsoluteThickness[2], Table[ Line[#[[i]], VertexColors -> (Blend[cols[[;; -2]], (# + a)/(2 a)] & /@ #[[i, ;; , 3]])], {i, Length[#]}] & /@ {dots, Transpose[dots]}}, Boxed -> False, PlotRange -> {{0, 2 ?}, {0, 2 ?}, {-2, 2}}, ImageSize -> 540, ViewPoint -> {2, 0, 1/2}, SphericalRegion -> True, Background -> cols[[-1]]], {?, 0, 2 ?}] ]

POSTED BY: Clayton Shonkwiler

4 Replies

Sort By:

EDITORIAL BOARD

EDITORIAL BOARD, WOLFRAM

Posted 6 years ago

- Congratulations! This post is now a Staff Pick as distinguished by a badge on your profile! Thank you, keep it coming, and consider contributing your work to the The Notebook Archive!

POSTED BY: EDITORIAL BOARD

Kuba Podkalicki

Posted 6 years ago

As usual great stuff! While it is not fun to write for everyone I knew I need to try to optimize it. To my surprise I was able to make it smooth and completely FE side which means you can use it e.g. as a progress indicator: \[CapitalPsi][m_, n_, {x_, y_}] := Sin[m \[Pi] x] Sin[n \[Pi] y]; DynamicModule[ {n = 20, a = 1.2, dots, cols = RGBColor /@ {"#0098d8", "#f54123", "#0b3536"}, \[Theta], colorGrid, cf}, dots = Table[{(we can pregenerate the table and leave z coordinate \ 'dynamic') 2 \[Pi] (x - 1)/n, 2 \[Pi] (y - 1)/n, Cos[Dynamic[ 2 Pi \[Theta]]] ((we are preparing 'dynamic placeholder' to \ be used later. the rescaling to 0-2Pi done here can be done FE side.) 1./Sqrt[2] \[CapitalPsi][3, 1, {(x - 1)/n, (y - 1)/n}] + 1/Sqrt[2] \[CapitalPsi][1, 3, {(x - 1)/n, (y - 1)/n}] ) }, {x, 1, n + 1}, {y, 1, n + 1}]; Overlay[{ Animator[ Dynamic[\[Theta]], AppearanceElements -> None, AnimationRate -> 1], Graphics3D[{ AbsoluteThickness[2], Table[With[{i = i}, Line[#[[i]], VertexColors -> ( Function[dynH, RGBColor[('manual blend' because FE can handle basic \ arithmetic and not Blend itself. InputForm/@RGBColor/@{"#0098d8", "#f54123","#0b3536"} ) 0.9607843137254902 (dynH + a)/(2. a), 0.596078431372549 + (0.2549019607843137 - 0.596078431372549) (dynH + a)/(2. a), 0.8470588235294118 + (0.13725490196078433 - 0.8470588235294118) (dynH + a)/(2. a) ], Listable ]@#[[i, ;; , 3]] )] ], {i, Length[#]} ] & /@ {dots, Transpose[dots]} }, Boxed -> False, PlotRange -> {{0, 2 \[Pi]}, {0, 2 \[Pi]}, {-2, 2}}, ImageSize -> 540, ViewPoint -> {2, 0, 1/2}, SphericalRegion -> True, Background -> cols[[-1]]] }, All, 2], Initialization :> (\[Theta] = 0) ]

As usual great stuff!

While it is not fun to write for everyone I knew I need to try to optimize it. To my surprise I was able to make it smooth and completely FE side which means you can use it e.g. as a progress indicator:

\[CapitalPsi][m_, n_, {x_, y_}] := Sin[m \[Pi] x] Sin[n \[Pi] y];
DynamicModule[
 {n = 20, a = 1.2, dots, 
  cols = RGBColor /@ {"#0098d8", "#f54123", "#0b3536"}, \[Theta], 
  colorGrid, cf},
 dots = Table[{(*we can pregenerate the table and leave z coordinate \
'dynamic'*)
    2 \[Pi] (x - 1)/n,
    2 \[Pi] (y - 1)/n,
    Cos[Dynamic[
       2 Pi \[Theta]]] ((*we are preparing 'dynamic placeholder' to \
be used later. the rescaling to 0-2Pi done here can be done FE side.*)


      1./Sqrt[2] \[CapitalPsi][3, 1, {(x - 1)/n, (y - 1)/n}] + 
       1/Sqrt[2] \[CapitalPsi][1, 3, {(x - 1)/n, (y - 1)/n}]
      )
    }, {x, 1, n + 1}, {y, 1, n + 1}];

 Overlay[{
   Animator[ Dynamic[\[Theta]], AppearanceElements -> None, 
    AnimationRate -> 1],
   Graphics3D[{
     AbsoluteThickness[2],
     Table[With[{i = i},
         Line[#[[i]], VertexColors -> (
            Function[dynH,

              RGBColor[(*'manual blend' because FE can handle basic \
arithmetic and not Blend itself. InputForm/@RGBColor/@{"#0098d8",
               "#f54123","#0b3536"} *) 
               0.9607843137254902 (dynH + a)/(2. a),

               0.596078431372549 + (0.2549019607843137 - 
                   0.596078431372549) (dynH + a)/(2. a),

               0.8470588235294118 + (0.13725490196078433 - 
                   0.8470588235294118) (dynH + a)/(2. a)
               ],
              Listable
              ]@#[[i, ;; , 3]]
            )]
         ],
        {i, Length[#]}
        ] & /@ {dots, Transpose[dots]}
     },
    Boxed -> False, 
    PlotRange -> {{0, 2 \[Pi]}, {0, 2 \[Pi]}, {-2, 2}}, 
    ImageSize -> 540, ViewPoint -> {2, 0, 1/2}, 
    SphericalRegion -> True, Background -> cols[[-1]]]
   }, All, 2],
 Initialization :> (\[Theta] = 0)
 ]

POSTED BY: Kuba Podkalicki