I have posted a similar question on StackOverflow (here), as it seems -- with the alleged exception of SimulationX -- to appear in System Modeler as well as in OpenModelica and Dymola. I believe that the issue may be of interest for this community and I would be very interested to see whether the issue is only related to System Modeler 4.3 (which I used for testing the issue) and what best can be done to avoid the sometimes tremendous errors within a model.
The Problem (minimum example)
I noted numerical errors trying to build a System Dynamics library where a component called "conveyor" typically is used to model the transport of an amount of some material from one stock to another using a fixed delay (also called pipeline delay in SD lingo). The issue seems closely related to event handling as becomes apparent especially when a pulse input is delayed, that uses time events in the Modelica standard library component:
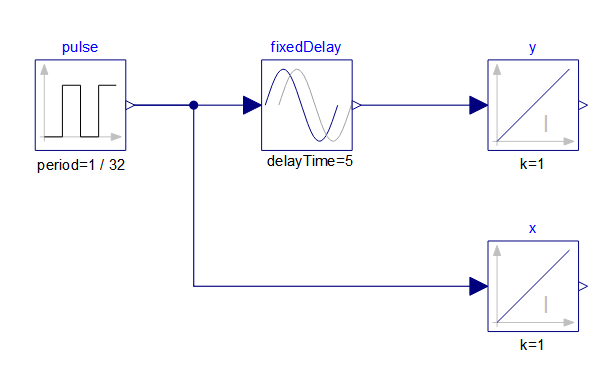
model PulseTest "Test FixedDelay with Pulse Input"
Modelica.Blocks.Nonlinear.FixedDelay fixedDelay( delayTime = 5 );
Modelica.Blocks.Sources.Pulse pulse(
startTime = 1,
width = 100,
period = 1/32,
amplitude = 32,
nperiod = 1
);
Modelica.Blocks.Continuous.Integrator x; // integrator for the undelayed pulse
Modelica.Blocks.Continuous.Integrator y; // integrator for the delayed pulse
equation
connect( pulse.y, fixedDelay.u );
connect( fixedDelay.y, y.u );
connect( pulse.y, x.u );
end PulseTest;
We have a pulse signal with amplitude a and a period (width = 100%) of 1/a which being integrated should eventually give 1.0 by the end of the simulation.
Simulating this simple model using DASSL from time 0 to 10 with standard settings (e.g. 2000 steps) will give these results:
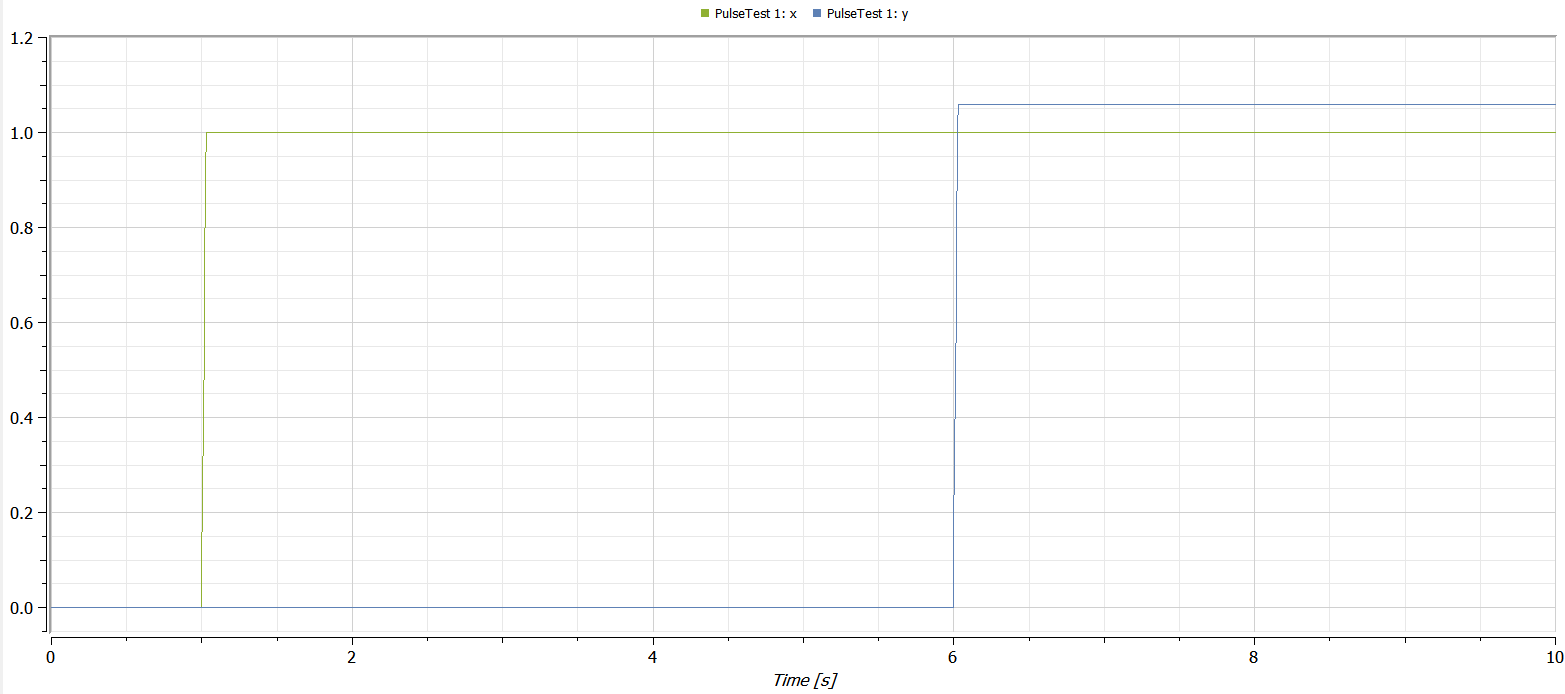
As we can see, the undelayed pulse correctly accumulates to 1.0 (x), while the delayed signal overshoots (y).
There is no easy way to fix this (greatly increasing the solver steps is one remedy) it seems. Euler fixed step for example correctly simulates the model, while the pulse disappears using Runge Kutta or Heun's method.
What is the best ("most robust and reliable") way to deal with this issue?
UPDATE (12/18/18):
Comments and a first answer by a Dymola developer give a confusing picture (cf. my post on SO): It seems that SimulationX, another commercial simulation environment for Modelica, will give the correct solution irrespective of solution method, while the Dymola developer states, that there is no easy workaround making event-propagation possible when choosing a variable step solver.