Dear Roman,
thank you very much for that fantastic post. I'll definitely have to get one of those pencils from somewhere. There is of course the following on question which is: What happens if we use different bases for our number system, i.e. binary numbers etc.
There is an obvious extension to all bases up to 10:
TruncatablePrimesbasis[p_Integer, basis_Integer] :=
With[{digits = IntegerDigits[p]},
h = FromDigits[ToString[p], basis];
If[PrimeQ[h], {p, TruncatablePrimesbasis[#, basis] & /@ (FromDigits /@ (Prepend[digits, #] & /@
Range[basis - 1]))}, {}]];
We can then generate all such strings for any base (up to 10):
generateAllStrings[basis_Integer] :=
DeleteDuplicates[SortBy[Flatten[TruncatablePrimesbasis[#, basis] & /@ (FromDigits /@ (List /@
Select[Range[basis - 1], PrimeQ]))], Length[IntegerDigits[#]] &]]
The following generates the table for the first few bases.
Transpose[Table[{k, generateAllStrings[k]}, {k, 2, 5}]] // Grid[#, Frame -> All] &

Note that for the binary system there is no such pencil/sequence. That is basically because the first prime is already two digits long, i.e. 10, and if I delete the first of the two digits I am left with 0 which is not prime.
It turns out that base 6 leads to a long list of strings (of course this contains all substrings of the same that are contained in longer strings), but basis 7 is surprisingly short:
generateAllStrings[7]
(*{2, 3, 5, 23, 25, 32, 43, 52, 65, 443, 452, 623, 625, 632, 652, 2452, \
2623, 6625, 6652, 42623, 642623, 6642623}*)
So, why did we stop at base 10. The issue is that for larger bases we need letters as digits. And we will probably need the function FromDigits that can transform an appropriate string into a number to any base up to 35 (which probably is because we then run out of letters in the alphabet). If we want to go to larger basis we have to work with strings rather than numbers. The updated program looks like this:
digitrange = Join[CharacterRange["1", "9"], CharacterRange["a", "z"]];
TruncatablePrimes[p_String, basis_Integer] :=
With[{digits = Characters[p]}, h = FromDigits[p, basis];
If[PrimeQ[h], {p, TruncatablePrimes[ToString[#], basis] & /@ (StringJoin[#] & /@ (Flatten[Prepend[digits, #]] & /@ (List /@ digitrange[[1 ;; basis - 1]])))}, {}]];
generateAllStrings[basis_Integer] :=
DeleteDuplicates[SortBy[Flatten[TruncatablePrimes[#, basis] & /@
Flatten[(List /@ Select[digitrange[[1 ;; basis - 1]], PrimeQ[FromDigits[#, basis]] &])]], StringLength[#] &]]
We can try this out like this:
Here is the longest string for base 11:
generateAllStrings[11][[-1]]
which gives a68822827.
FromDigits["a68822827", 11]
shows that this is 2276005673 which is prime. (Try PrimeQ). We can now slice off one digit by one:
Table[FromDigits[StringTake[#, -k], 11] & @"a68822827", {k, 9, 1, -1}]
and get
{2276005673, 132416863, 15493837, 1321349, 32941, 3659, 997, 29, 7}
all of which are prime. It turns out that for some bases the strings are much longer than for others ( I haven't finished calculating for basis 18 for example!). Here is what we can do:
Monitor[data = Table[{k, Length[#], StringLength[#[[-1]]], #[[-1]]} &@generateAllStrings[k], {k, 3, 17}], k]
So we save the base, the total number of sequences, the longest string length (not necessarily a unique string), and the longest string. Here is the table:
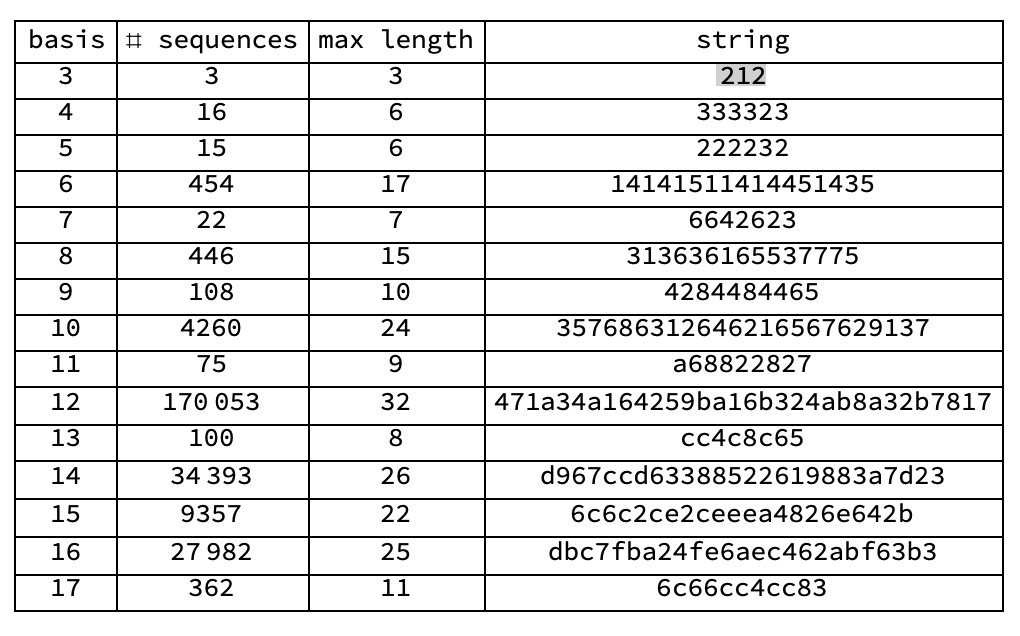
This shows the length of the longest sequence vs base:
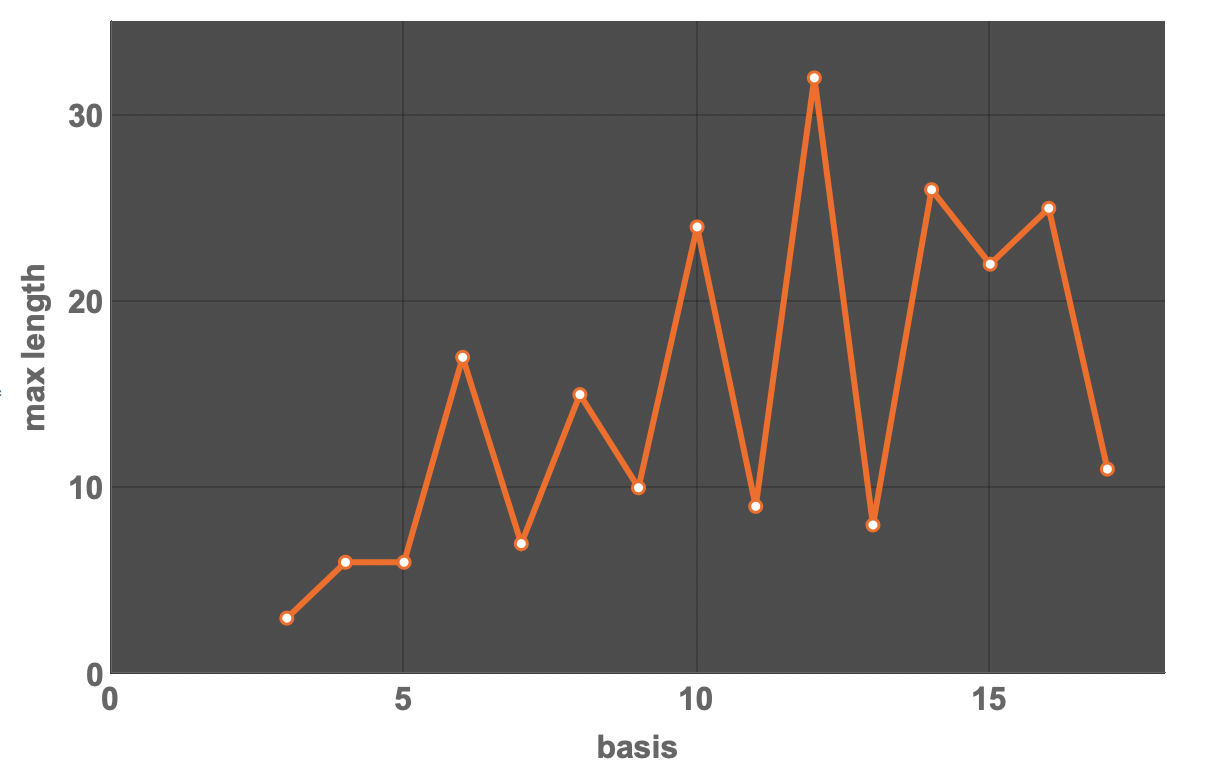
I will try to calculate the sequences for some larger bases. As I said 18 has not finished yet. 19 is fast and short. 20 seems to take long, too. In fact, I think that it might be possible to speed this program up quite a bit, which I might want to do first....
Thanks a lot for this very nice post.
Cheers,
Marco