Dear Hafez,
the idea is really simple. EdgeStyle colours an edge - the edge needs to be given by a pair of numbers (the two vertices that are linked).
If we write
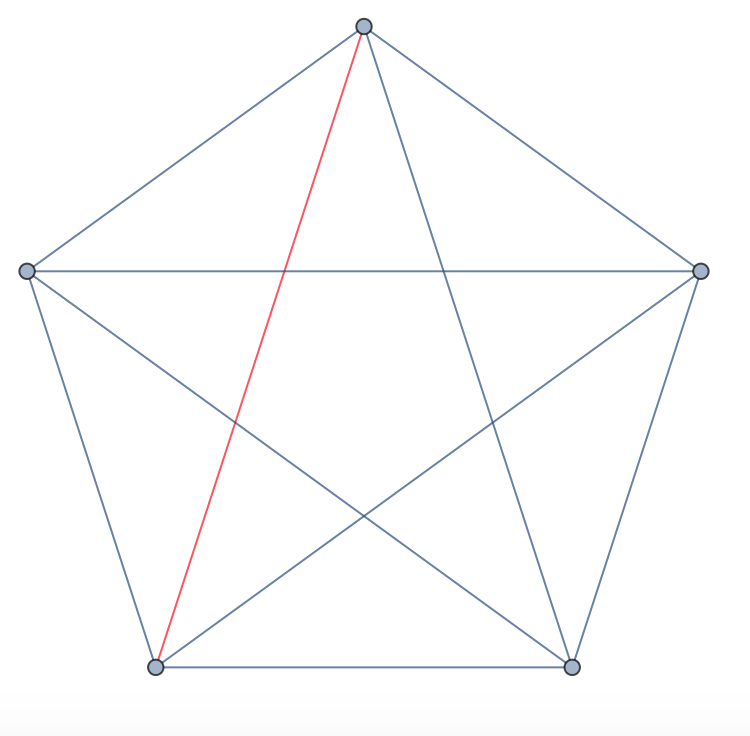
CompleteGraph[5, EdgeStyle -> {1 \[UndirectedEdge] 3 -> Red}]
that colours the edge from node 1 to 3:
Next, it would be good to know what the vertex labels/names are (if you do not know it already):
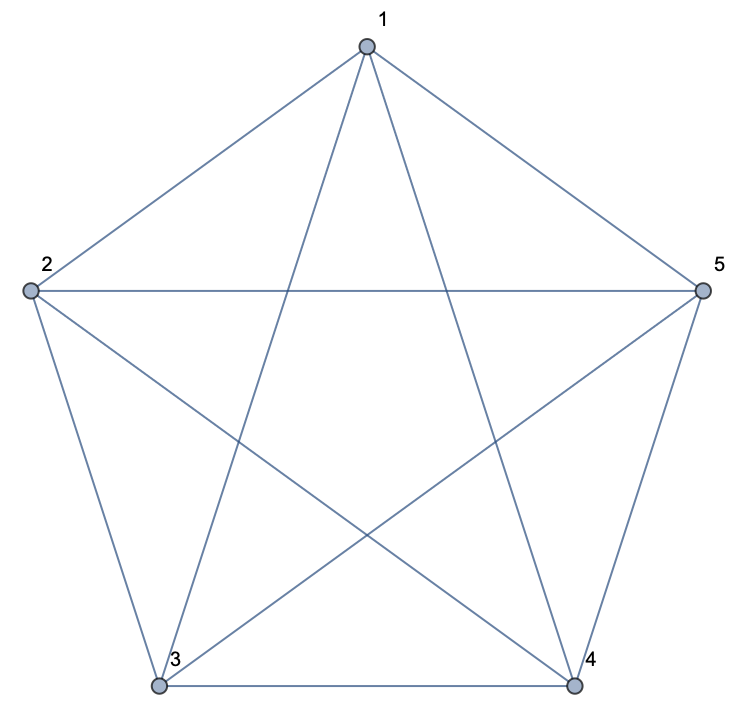
CompleteGraph[5, VertexLabels -> "Name"]
So I want to highlight the edges from 1 to 3; 2 to 4; 3 to 5; 4 to 1; 5 to 2.
It is practically linking each vertex to the one with the index two higher, until I come to vertices 4 and 5, which are linked to 1 and 2 respectively. This is because the situation is modulo 5 (i.e. circular).
So I could write:
CompleteGraph[5, EdgeStyle -> {1 \[UndirectedEdge] 3 -> RGBColor[1, 0, 0],
2 \[UndirectedEdge] 4 -> RGBColor[1, 0, 0],
3 \[UndirectedEdge] 5 -> RGBColor[1, 0, 0],
4 \[UndirectedEdge] 1 -> RGBColor[1, 0, 0],
5 \[UndirectedEdge] 2 -> RGBColor[1, 0, 0]}]
and that would do the trick. I am just terribly lazy; so I did not want to type all of that in. The table that I use generates exactly the list that I use for EdgeStyle. Writing the EdgeStyle programatically also has the advantage that this generalises easily:
For example:
CompleteGraph[23, EdgeStyle -> Flatten[Table[k \[UndirectedEdge] Mod[k + 1, 23] + 1 -> Red, {k, 1, 23}]]]

You can also produce graphs where all the edges that correspond different (vertex index) distance are coloured differently:
CompleteGraph[17,
EdgeStyle ->
Flatten[Table[colour = RandomColor[];
Table[k [UndirectedEdge] Mod[k + j, 17] + 1 -> colour, {k, 1,
17}], {j, 1, 15}]], VertexLabels -> "Name"]
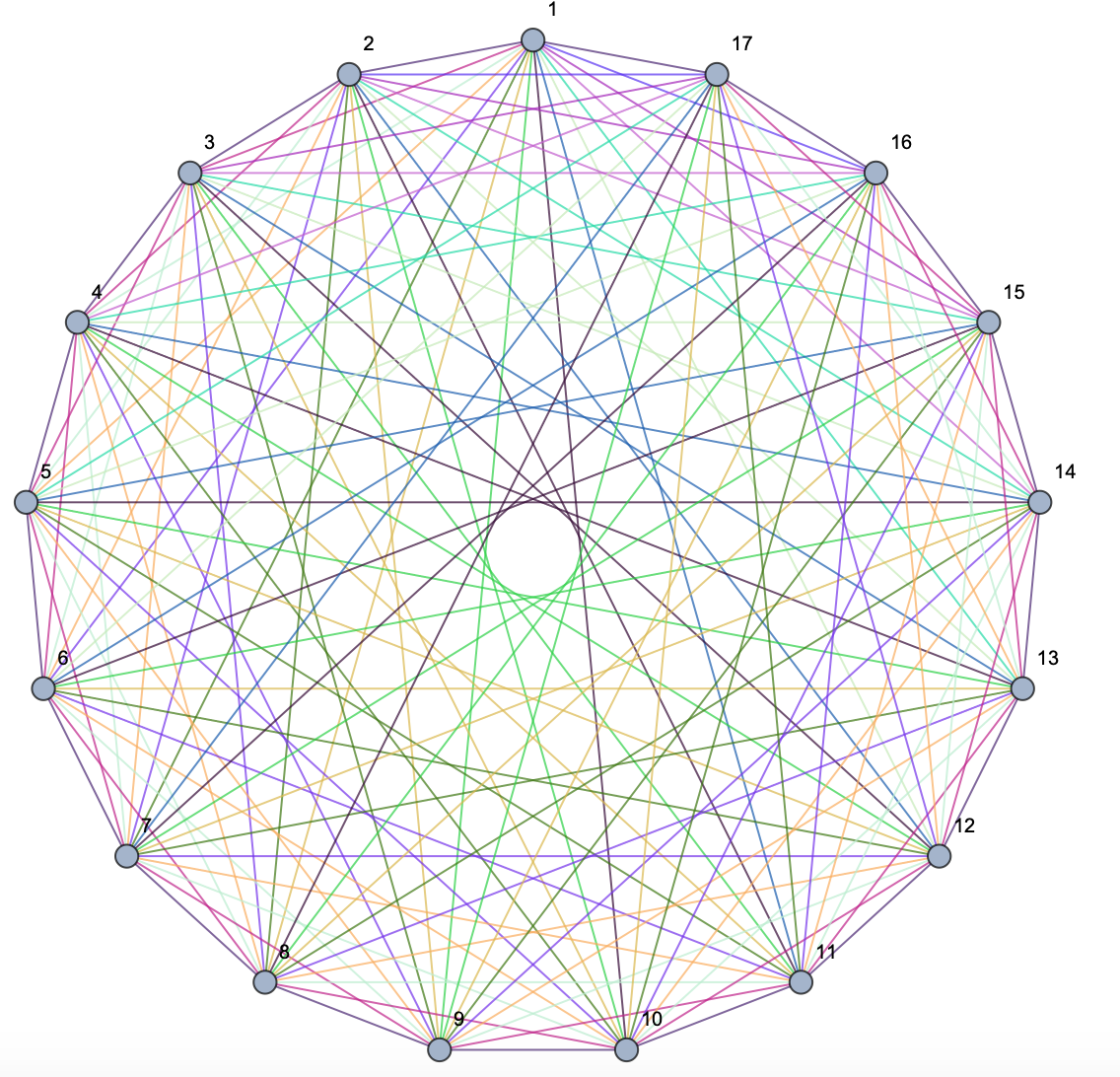
Note that it will "write-over" some distances.... this is just an illustration.
Cheers,
Marco