Hi Markus,

Take a look at the PeriodicBoundaryCondition>Scope>2D PDE Problems for an example on how to set up a PBC. Execute this code after you execute your code to see one possible implementation.

<< NDSolve`FEM`
\[CapitalOmega] = Rectangle[{0, 0}, {2 * \[CapitalLambda] , Lz}];
pde = -\!\(
\*SubsuperscriptBox[\(\[Del]\), \({x, z}\), \(2\)]\(u[x, z]\)\) == 0;
Subscript[\[CapitalGamma], D] = 
  DirichletCondition[
   u[x, z] == T0x[x], (z == 0) && 0 < x <= 2 * \[CapitalLambda] ];
Subscript[\[CapitalGamma], D2] = 
  DirichletCondition[
   u[x, z] == T0, (z == Lz) && 0 < x <= 2 * \[CapitalLambda]];
mesh = ToElementMesh[\[CapitalOmega], 
   "MaxBoundaryCellMeasure" -> 0.000001];
f = TranslationTransform[{2 * \[CapitalLambda], 0}];
pbc = PeriodicBoundaryCondition[u[x, z], x == 0, f];
ufun = NDSolveValue[{pde, pbc, Subscript[\[CapitalGamma], D], 
    Subscript[\[CapitalGamma], D2]}, u, {x, z} \[Element] mesh];
ContourPlot[ufun[x, z], {x, z} \[Element] mesh, MaxRecursion -> 4, 
 Contours -> 30, ColorFunction -> "BlueGreenYellow", 
 FrameStyle -> Directive[Black, Thickness[0.003]], 
 LabelStyle -> Directive[Black, 10], 
 FrameLabel -> {"x [m]", "z [m]"} ]

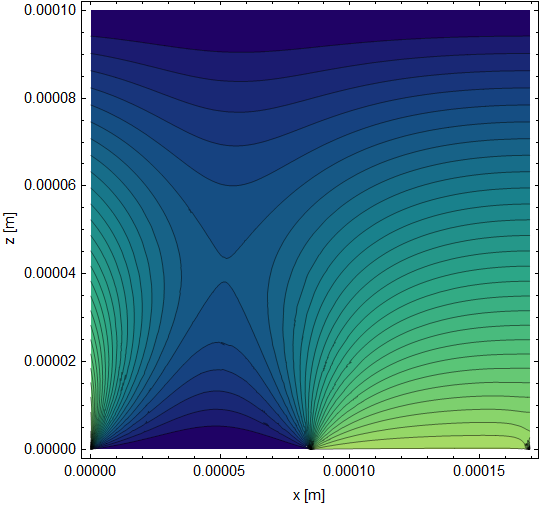
Compared to one period (the 5th to 6th) of your solution plotted using the following.

ContourPlot[
 us[x, z], {x, 5 2 \[CapitalLambda], 6 2 \[CapitalLambda]}, {z, 0, 
  Lz}, Contours -> 30, MaxRecursion -> 4, 
 ColorFunction -> "BlueGreenYellow", PlotPoints -> 200, 
 FrameStyle -> Directive[Black, Thickness[0.003]], 
 LabelStyle -> Directive[Black, 10], FrameLabel -> {"x [m]", "z [m]"}]

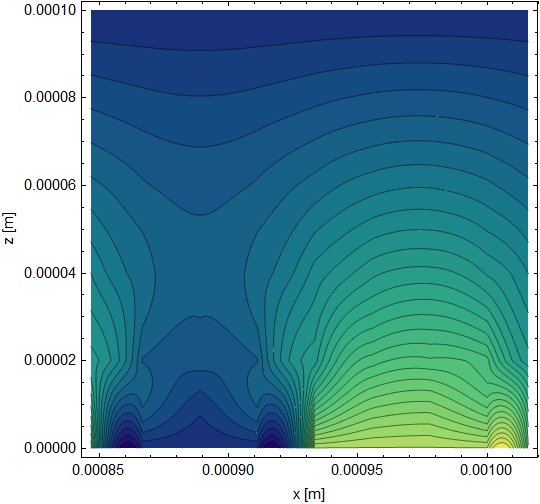
Your current solution has some sharp features that I would not expect in a diffusion problem. In contrast, the periodic solution is smooth when you get away from boundary effects.

You can use the attached in case the formatting gets mucked up in the post due to special characters.

Also, MaxRecursion can be used to smooth out the plots, but it can take some time if the plot is complex.

Attachments:

heat distributio...nb

Hi Markus,

You could just define a function that shifts the contour plot and then seam them together with Show. For example:

cp[i_, n_] := 
  ContourPlot[
   ufun[x - 2*\[CapitalLambda] i, z], {x, 2*\[CapitalLambda]*i, 
    2*\[CapitalLambda]*(i + 1)}, {z, 0, Lz}, MaxRecursion -> 4, 
   Contours -> 30, ColorFunction -> "BlueGreenYellow", 
   FrameStyle -> Directive[Black, Thickness[0.003]], 
   LabelStyle -> Directive[Black, 10], 
   FrameLabel -> {"x [m]", "z [m]"} , 
   PlotRange -> {{0, 2 * \[CapitalLambda] * (n)}, {0, Lz}}];
nplts = 5;
Show[Table[cp[i, nplts], {i, 0, nplts - 1}]]

Best regards and Happy New Year!

Tim

You're welcome Markus!

Good catch.

The following is an alternative way to create the stitched together graphic using Translate.

cplot = ContourPlot[
   ufun[x, z], {x, 0, 2*\[CapitalLambda]}, {z, 0, Lz}, 
   MaxRecursion -> 4, Contours -> 30, 
   ColorFunction -> "BlueGreenYellow" ];
n = 5;
Graphics[Table[
  Translate[First@cplot, {2 \[CapitalLambda] i, 0}], {i, 0, n}], 
 PlotRange -> {{0, 2 * \[CapitalLambda] * n}, {0, Lz}}, Frame -> True,
  FrameStyle -> Directive[Black, Thickness[0.003]], 
 LabelStyle -> Directive[Black, 10], FrameLabel -> {"x [m]", "z [m]"},
  AspectRatio -> 1]

Update

In the link that I provided, they actually show an example of how to stitch PBC problems together in the basic examples section. It probably is the simplest as shown below.

cplot = ContourPlot[
   ufun[x, z], {x, 0, 2*\[CapitalLambda]}, {z, 0, Lz}, 
   MaxRecursion -> 4, Contours -> 30, 
   ColorFunction -> "BlueGreenYellow", 
   FrameStyle -> Directive[Black, Thickness[0.003]], 
   LabelStyle -> Directive[Black, 10], 
   FrameLabel -> {"x [m]", "z [m]"} ];
n = 5;
Show[Table[
  MapAt[Translate[#, {2 \[CapitalLambda] i, 0}] &, cplot, 1], {i, 0, 
   n}], PlotRange -> All]

Attached is a corrected notebook include the shift noted by Markus.

Attachments:

heat distributio...nb