I've reduced my problem to $H(w) = \dfrac{1}{(1-\frac{1}{4}e^{-jw})(1-\frac{1}{3}e^{-jw})}$. I need its inverse discrete Fourier transform.

My thinking is that I could use partial fraction decomposition to break this into two fractions of the form $\dfrac{1}{(1-ae^{-jw})}$ which I can then inverse Fourier transform to get a result of the form $h[n] = a^nu[n]$

To simplify, I let $S = e^{-jw}$

Thus $H(w) = \dfrac{1}{(1-\frac{1}{4}e^{-jw})(1-\frac{1}{3}e^{-jw})}$ becomes $H(w) = \dfrac{1}{(1-\frac{1}{4}S)(1-\frac{1}{3}S)}$

I tried to work these and both answer are different:

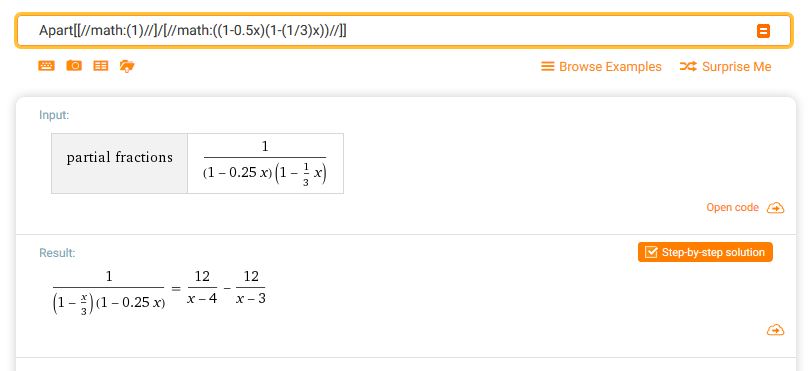
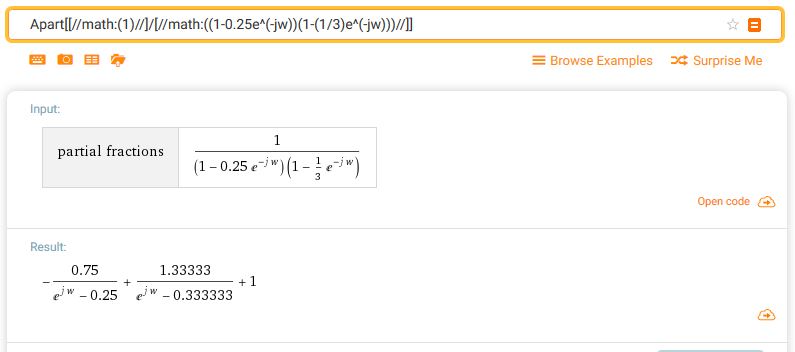
SHouldn't these be equal? If so, I cannot figure out the necessary steps to get from one to the other. Any help would be appreciated.