It should be noted that z1 is a vector {z1[[1]],z1[[2]]}. The signs of the remaining expressions can be clarified.
z1 = {-R*W*Sin[W*t] + l'[t]*Sin[\[Phi][t]] +
l[t]*(\[Phi]'[t])*Cos[\[Phi][t]],
R*W*Cos[W*t] - l'[t]*Cos[\[Phi][t]] +
l[t]*(\[Phi]'[t])*Sin[\[Phi][t]]};
V = m*g*(R*Sin[W*t] - l[t]*Cos[\[Phi][t]]) + 1/2*k*(l[t] - l0)^2;
T = 1/2*m*z1.z1;
Lagrange = T - V;
eqs = D[D[Lagrange, \[Phi]'[t]], t] - D[Lagrange, \[Phi][t]];
eqs2 = D[D[Lagrange, l'[t]], t] - D[Lagrange, l[t]];
g = 9.7; m = 1; l0 = 1; k = 1000; R = 2; W = Pi/2;
sol = NDSolveValue[{eqs == 0, eqs2 == 0, l[0] == l0, l'[0] == 0,
Derivative[1][\[Phi]][0] == 0, \[Phi][0] == 0}, {l[t], \[Phi][
t]}, {t, 0, 20}]
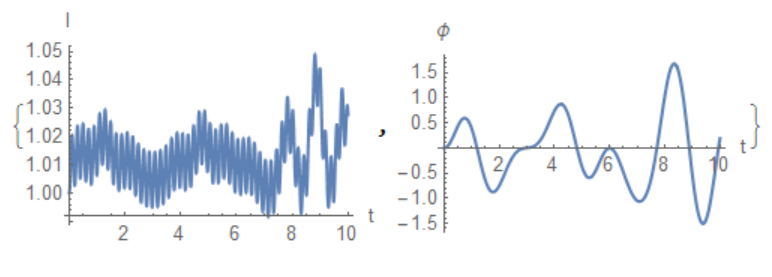
{Plot[sol.{1, 0}, {t, 0, 10}, AxesLabel -> {"t", "l"}],
Plot[sol.{0, 1}, {t, 0, 10}, AxesLabel -> {"t", "\[Phi]"}]}