So I'm having an issue where the RegionCentroid operation does not compute even though I've used it successfully many times in the past.
Here are the coordinates of the shape I'm trying to determine the centroid for:
C1 = {-0.82998570, 0.39131282, 1.38566726}
C2 = {-0.01947705, -0.00824240, 2.45464906}
C3 = {1.21666293, -0.61144232, 2.04941022}
C4 = {1.35625427, -0.67525738, 0.64442667}
S = {-0.01598580, -0.00235848, -0.00262605}
Here I'm building the Polygon:
Plane= Polygon[{C1, C2, C3, C4, S}]
And here is what what I'm using to determine the centroid of the region:
OO=RegionCentroid[Plane]
This is an issue I'm experiencing in Mathematica 11.3. That exact line of commands worked fine in Mathematica 10. I'm getting the error message shown below. 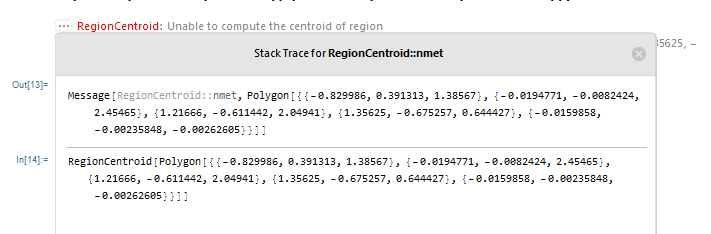
Any ideas as to why this is happening and how to fix it?
Thanks!