I notice one issue: I think the setup isn't quite correct. Symmetry suggests that the B-field in the x-y plane should only be in the z-direction.
Given the Biot-Savart law, I get as my integrand
(\[Mu]0 mI)/(4 \[Pi])
Cross[{-a Sin[\[Theta]], a Cos[\[Theta]], 0}, {x - a Cos[\[Theta]],
y - a Sin[\[Theta]], 0}]/
Norm[{x - a Cos[\[Theta]], y - a Sin[\[Theta]], 0}]^3 // Simplify
{0, 0, (a mI \[Mu]0 (a - x Cos[\[Theta]] - y Sin[\[Theta]]))/(
4 \[Pi] (Abs[x - a Cos[\[Theta]]]^2 + Abs[y - a Sin[\[Theta]]]^2)^(
3/2))}
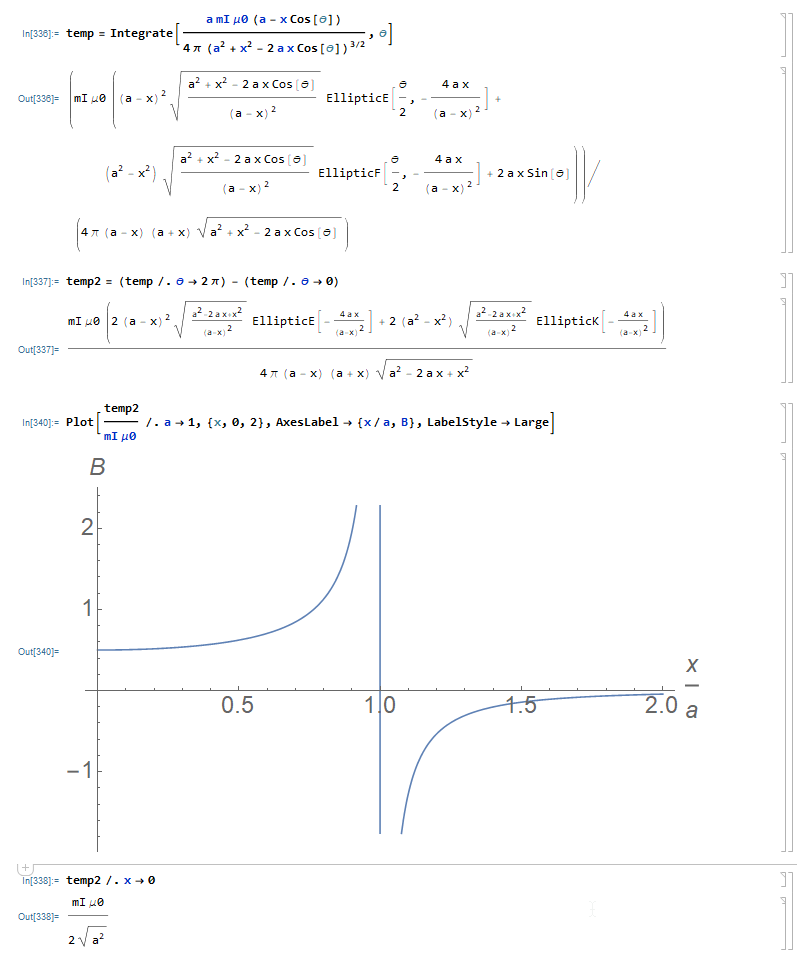
Now, because of the symmetry of our situation, I assume without loss of generality that y=0. Now I do an indefinite integral (because for whatever reason the definite integral still seems to hang after this assumption), and I have
temp = Integrate[(a mI \[Mu]0 (a - x Cos[\[Theta]]))/(
4 \[Pi] (a^2 + x^2 - 2 a x Cos[\[Theta]])^(3/2)), \[Theta]];
temp2 = (temp /. \[Theta] -> 2 \[Pi]) - (temp /. \[Theta] -> 0)
This returns an answer in terms of EllipticE and EllipticK. As a sanity check, I verify that the field at the origin is as expected,
In[5]:= temp2 /. x -> 0
Out[5]= (mI \[Mu]0)/(2 Sqrt[a^2])
and that the field displays the expected behavior as x goes to a, namely that it should be positive, diverge at the coil, and then go negative.