I would like to share with Wolfram Community an article I wrote recently. The original can be found at my blog ACA Death Spiral with Mathemtica notebook available for download here.

According to a news report from Reuters, which is being picked up widely, early figures from four states are suggesting that the pool of insureds enrolling in the Exchanges is older than anticipated. If this situation persists and is not an artifact of either the particular states involved or simply the urgency with which older people applied, it further threatens the ability of the Affordable Care Act to sustain its plan of equalizing opportunity to acquire health insurance. This is so because, although older people do pay more in the Exchanges established by the Affordable Care Act, they pay less than would be actuarially appropriate. Young people, by contrast, pay more.

Here’s the key passage from the Reuter’s report.

A back of the envelope computation shows that this situation could result in additional losses of about 10% by insurers before risk adjustment payments are taken into account. And this is true even if each age group in the pool is as healthy as anticipated. The insurer losses resulting from disproportionate enrollment of older insureds has several important consequences: (1) insurers may decide to exit the pool in the future; (2) insurers may decide to raise premiums to adjust to the real pool as opposed to the projected pool; and (3) the government is going to pay more in Risk Corridor payments than anticipated.






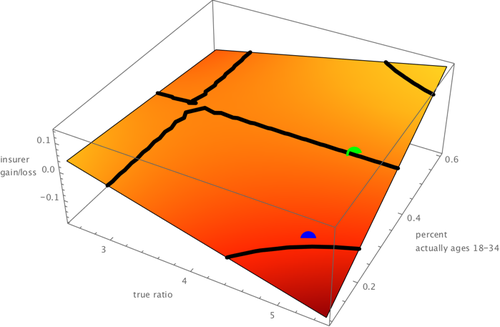Relationship between “true ratio”, percent young in the pool, and Exchange insurer profitability

The graphic above attempts to explain the issue. The x-axis shows the “true ratio” of expected medical claims to be paid between the oldest people in the pool and the expected medical claims to be paid of the youngest people in the pool. No one knows this figure for sure, but it could well be about 5 to 1. (This is why the Affordable Care Act is forced to hold premiums to a 3 to 1 ratio; otherwise premiums for the older group would be extremely high.) The y-axis shows the percentage of people entering the Exchange pools who are between 18 and 35. As the Reuters story indicates, it was hoped this group would comprise 38% of the pool. The green dot shows the result that might be hoped for if the young (18-35) indeed constitute 38% of the pool and the true ratio of claims paid between oldest and youngest is 5 to 1. At this level, insurers neither make unusual profits nor suffer unusual losses. The blue dot shows the result that might be seen if the young end up constituting — as the Reuters says the early evidence shows — about 20% of the pool. As one can see the red dot produces losses that are close to 10% of the risk assumed by insurers.

I’m placing a Mathematica notebook on Dropbox showing the computation. The idea, is that one finds a linear relationship between age and premium relationship that just covers claims payments for any value of the true ratio but subject to the constraint that the premium the oldest person pays can not be more than three times bigger than the premium the youngest person pays and under the assumption that those under age 35 constitute 38% of the pool. One then determines profits for any combination of true ratio and percentage of the pool under age 35. The process takes a little algebra (mostly rescaling operations), some calculus (finding “expectations” of distributions) and some visualization.

N O T E S

1. Although I modeled it that way, I am fully aware that the relationship between age and claims is non-linear. It’s probably more cubic. I’m also fully aware the relationship between age and premiums tends not to be linear under the Affordable Care Act. You can use the wonderful Kaiser Calculator or go to the fabulous Health Sherpa website to see that. And I’m also aware that using a uniform distribution to model the distribution of ages within the 18-35 group and the 35-64 group is imperfect. Still, for purposes of getting just some rapid order of magnitude estimates to guard against those who would dismiss the problem or wildly exaggerate it, I believe the linear assumption is supportable. It keeps things simple in a situation in which one has to be very careful about false assertions of precision and in which predictions are often hideously wrong.

2. As mentioned earlier, if the disproportionate enrollment of the elderly does not persist, as supporters of the ACA hope, the problem identified in this entry is reduced. Other problems, such as disproportionate enrollment of the unhealthy — which is a far more significant issue — may persist. But we don’t have data at present on the health of those enrolling. It is troublesome, however, that most of the time proponents of the ACA trot out someone who has actually enrolled in the Exchanges (or is a Jessica Sanford who thought they would), it is someone who has higher-than-average medical expenses. I wish they would more frequently show off someone who is healthy now but just wants protection against the possibility of an adverse health event.