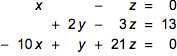The typical alignment tools for 2D alignment are
Grid and
GridBox. These can be created by code or by typing "Ctrl+," and "Ctrl+Enter". Looking at your example it seems you would like to lay out the system in a text cell.
If you use the "Ctrl" method, it works pretty well. You get the default spacing and alignment, which may be good enough. You can use the menu command Cell > ShowExpression to edit the
GridBox options in the text cell to get the alignment just right. It can be a pain to edit, especially if you accidentally mess up the whole cell. The editor is not as user-friendly as the normal code editor, either.
You can also create a
GridBox in code and paste it into a text cell. Each term is typeset with three elements, an operation (+/-), a coefficient (the absolute value), and a variable. An initial + is omitted. A coefficient of 1 is also omitted. And not every variable appears need appear in each equation. The one problem with the code below is that if all the equations begin with positive coefficients, the first column is full of blank and might be omitted; but the code below does not remove it.
ClearAll[layoutLHS];
(*
assumes the form of an equation is that the terms to be aligned
are all on the left hand side, each term consisting of an optional
coefficient and a variable
*)
layoutLHS::usage = "layoutLHS[{a1 x1 + a2 x2 + ... == A, b1 x1 + b2 x2 + ... == B, ...}, {x1, x2, ...}]";
layoutLHS[eqns : {(Plus[__] == _) ..}, alignmentForms_List] :=
Module[{
pos = (* a table of Rules: var -> position index *)
Thread[alignmentForms -> Range@ Length@ alignmentForms] ~Join~ {_ -> -1},
lhs, (* left hand side of eqn *)
rhs, (* right hand side of eqn *)
row, (* a row in the grid *)
nvars = Length@alignmentForms}, (* number of variables *)
FormBox[
GridBox[
Function[{eq}, (* creates a row for the grid from each equation *)
{lhs, rhs} = List @@ eq;
lhs = List @@ lhs; (* replaces Plus with List *)
row = ConstantArray["", 3 nvars + 2]; (* initialize row to have empty entries *)
row[[{-2, -1}]] = {"=", rhs}; (* insert the "=" and right hand side into the row *)
(* converts each term of the LHS to a three elements, sign, coeff, variable, of the Grid *)
Scan[ (* updates the entries of row with terms that appear in the equation eq *)
With[{found = First@ Cases[#, Alternatives @@ alignmentForms, {0, Infinity}] /. pos}, (* find the variable in this term *)
If[#/alignmentForms[[found]] < 0, (* operation sign +/- *)
row[[3 found - 2]] = "-",
If[found > 1, row[[3 found - 2]] = "+"]]; (* no + for first term *)
If[found > 0,
row[[{3 found - 1, 3 found}]] = {Abs[#/alignmentForms[[found]]] /. 1 -> "", (* abs. coeff *)
ToBoxes@ alignmentForms[[found]]}] (* variable *)
] &,
lhs (* scans the left hand side *)
];
row (* output the row *)
] /@ eqns,
(* we put the coeffs. closer to the vars. (the 0.2 below) *)
ColumnSpacings -> Flatten[ConstantArray[{0.8, 0.2, 0.8}, nvars] ~Append~ 0.8],
ColumnAlignments -> Right
], TraditionalForm]
]
Example: To make a cell out of the output of
layoutLHS, we wrap it in
BoxData and put it in
Cell, with an appropriate style such as
Text. We can then create a cell with
CellPrint.
CellPrint[
Cell[BoxData@
layoutLHS[{x - z == 0, 2 y - 3 z == 13, -10 x + y + 21 z == 0}, {x, y, z}], "Text"]]