
For a calculus assignment, I was asked to calculate the volume of a pastry that could be modeled as a solid of revolution. For this sweet math exercise, I picked an oddly shaped blueberry muffin. The goal is to find the single variable function that can be rotated around an axis to form the muffin, then integrate it for a full rotation.
Initially, I cropped the image and turned it to its side:

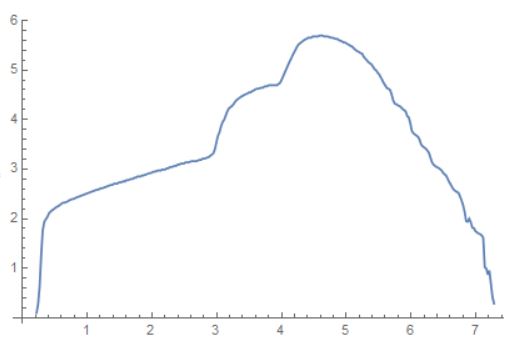
Next, I used EdgeDetect on a binarized version of the image and plotted the resulting list of points on the edge. I adjust the width of the curve so it accounts for the 11.4cm maximum diameter of the muffin I measured by hand :
points = SortBy[
KeyValueMap[List,
N[Mean /@
GroupBy[PixelValuePositions[
EdgeDetect@DeleteSmallComponents@Binarize[i], 1],
First -> Last]]], First]/41.7544`;
ListLinePlot[points]
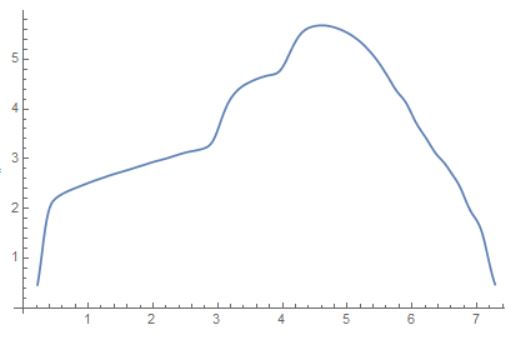
To get rid of the irregularity, I used a GaussianFilter on the points:
smoothPoints =
Transpose[{points[[All, 1]], GaussianFilter[points[[All, 2]], 6]}];
ListLinePlot[smoothPoints]
To make my muffin curve actually differentiable, I turned the list of points into a polynomial function that represents the muffin:
ipf = Interpolation[smoothPoints]
terms = Table[
2/\[Pi] NIntegrate[
ipf[Rescale[
x, {-1, 1}, {Min[smoothPoints[[All, 1]]],
Max[smoothPoints[[All, 1]]]}]] ChebyshevT[n, x]/Sqrt[
1 - x^2], {x, -1, 1}], {n, 0, 25}];
poly = Expand[-First[terms]/2 +
Evaluate[terms.Table[ChebyshevT[n - 1, x], {n, Length[terms]}]]]
The result was this beauty:
4.63236 + 1.20442 x + 25.4792 x^2 + 221.382 x^3 - 1054.27 x^4 - 4867.47 x^5 + 15974.6 x^6 + 52135.3 x^7 - 130554. x^8 - 338152. x^9 + 649051. x^10 + 1.4346310^6 x^11 - 2.09110^6 x^12 - 4.1356810^6 x^13 + 4.504910^6 x^14 + 8.2375510^6 x^15 - 6.5474610^6 x^16 - 1.1333410^7 x^17 + 6.3353710^6 x^18 + 1.0567110^7 x^19 - 3.9089610^6 x^20 - 6.370710^6 x^21 + 1.3906910^6 x^22 + 2.23971*10^6 x^23 - 216984. x^24 - 348587. x^25
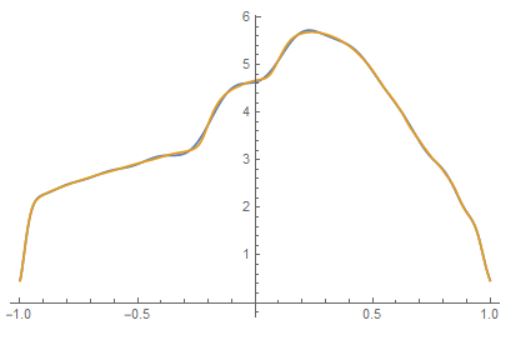
To compare the two curves by plotting them on the same axes:
Plot[{poly,
ipf[Rescale[x, {-1, 1}, MinMax[smoothPoints[[All, 1]]]]]}, {x, -1,
1}]
As you notice the x-axis dimension needs to be adjusted back to the original width to height ratio of the picture:
scaledpoly =
poly /. x -> Rescale[x, MinMax[smoothPoints[[All, 1]]], {-1, 1}]
4.63236 + 1.20442 (-1.06102 + 0.283081 x) + 25.4792 (-1.06102 + 0.283081 x)^2 + 221.382 (-1.06102 + 0.283081 x)^3 - 1054.27 (-1.06102 + 0.283081 x)^4 - 4867.47 (-1.06102 + 0.283081 x)^5 + 15974.6 (-1.06102 + 0.283081 x)^6 + 52135.3 (-1.06102 + 0.283081 x)^7 - 130554. (-1.06102 + 0.283081 x)^8 - 338152. (-1.06102 + 0.283081 x)^9 + 649051. (-1.06102 + 0.283081 x)^10 + 1.4346310^6 (-1.06102 + 0.283081 x)^11 - 2.09110^6 (-1.06102 + 0.283081 x)^12 - 4.1356810^6 (-1.06102 + 0.283081 x)^13 + 4.504910^6 (-1.06102 + 0.283081 x)^14 + 8.2375510^6 (-1.06102 + 0.283081 x)^15 - 6.5474610^6 (-1.06102 + 0.283081 x)^16 - 1.1333410^7 (-1.06102 + 0.283081 x)^17 + 6.3353710^6 (-1.06102 + 0.283081 x)^18 + 1.0567110^7 (-1.06102 + 0.283081 x)^19 - 3.9089610^6 (-1.06102 + 0.283081 x)^20 - 6.370710^6 (-1.06102 + 0.283081 x)^21 + 1.3906910^6 (-1.06102 + 0.283081 x)^22 + 2.23971*10^6 (-1.06102 + 0.283081 x)^23 - 216984. (-1.06102 + 0.283081 x)^24 - 348587. (-1.06102 + 0.283081 x)^25
Another look at our plot:
Plot[{scaledpoly}, {x, Min[smoothPoints[[All, 1]]],
Max[smoothPoints[[All, 1]]]}]
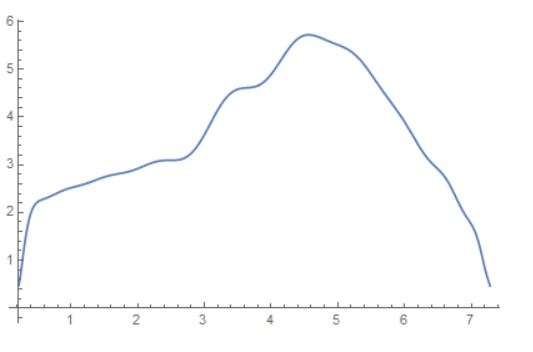
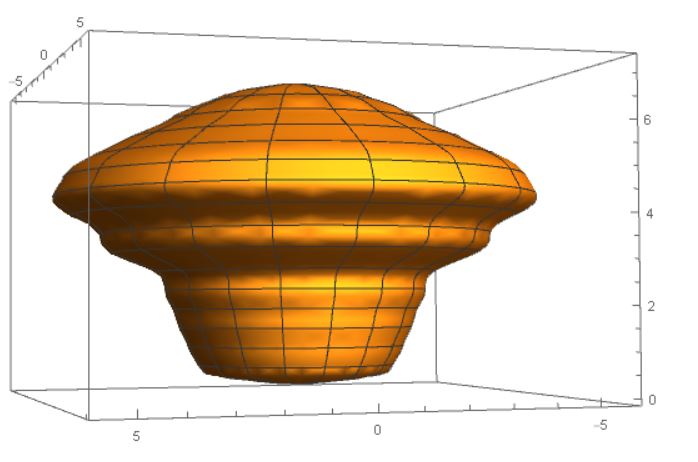
Perfect, we're now ready to rotate and integrate our curve:
RevolutionPlot3D[scaledpoly, {x, Min[smoothPoints[[All, 1]]],
Max[smoothPoints[[All, 1]]]}, RevolutionAxis -> {1, 0, 0}]

NIntegrate[\[Pi] scaledpoly^2, {x, Min[smoothPoints[[All, 1]]],
Max[smoothPoints[[All, 1]]]}]
325.81
The solution we were looking for are 325.81 cm^3 of delicious muffin.
If you are curious to know how close this is to the value I obtained by cutting up and measuring slices of the muffin, check out the attached notebook.
Otherwise, thank you for reading and rest assured no food was wasted in the production of this exploration.
 Attachments:
Attachments: