I have tried to implement the so-called Max-Plus algebra
http://en.wikipedia.org/wiki/Max-plus_algebrain Mathematica.
The basic operations can be implemented easily
x_\[CirclePlus]y_ := Max[x, y]
x_\[CircleTimes]y_ := x + y
It appears that the matrix product in max-plus can be easily implemented in principle using
x_\[CircleDot]y_ := x.y /. Plus -> Max /. Times -> Plus
When I multiply two matrices such as
A = {{a, b}, {c, d}};
B = {{e, f}, {g, h}};
This works fine:
A\[CircleDot]B // MatrixForm
[font=Arial, 'Arial Narrow', Helvetica, Verdana, sans-serif]
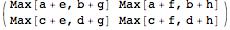
The first problem occurs when I square a matrix:
A\[CircleDot]A // MatrixForm
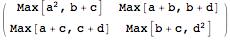
Because of the inner workings of the Dot[] function there is an a^2 which should be an a+a. I can fix that by changing the definition of the max-plus dot product to
x_\[CircleDot]y_ :=
x.y /. Plus -> Max /. Times -> Plus /. Power -> Times
Then
A\[CircleDot]A // MatrixForm
gives
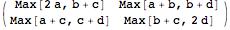
.
All of this becomes more complicated when we use numbers in the definition of A, e.g.
A = {{4, 3}, {7, -Infinity}}
Now A^2 gives
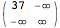
instead of

I have tried all sorts of Unevaluate, Hold, HoldAll etc commands, but it appears that Dot[] is so deep within the language that its constitutents are difficult to substitute. Does anyone have a good idea how to use this principle to get the max plus matrix multiplication right?
PS: I am aware that I can define max-plus matrix multiplication in ways that are not based on the standard Dot[] function.