Message Boards Message Boards

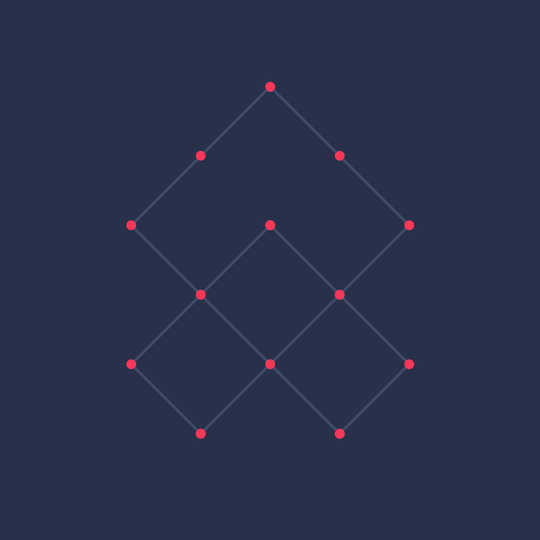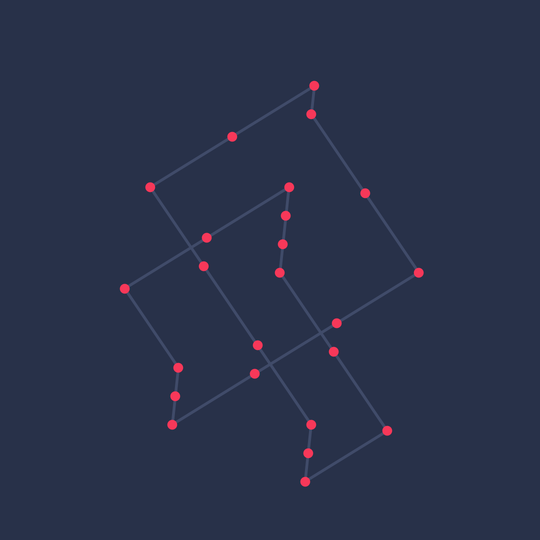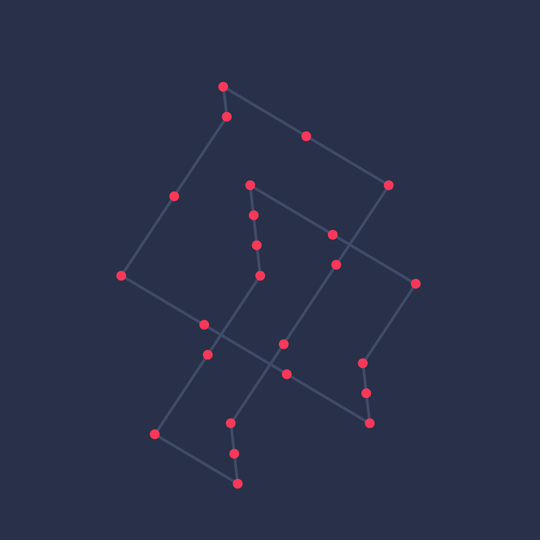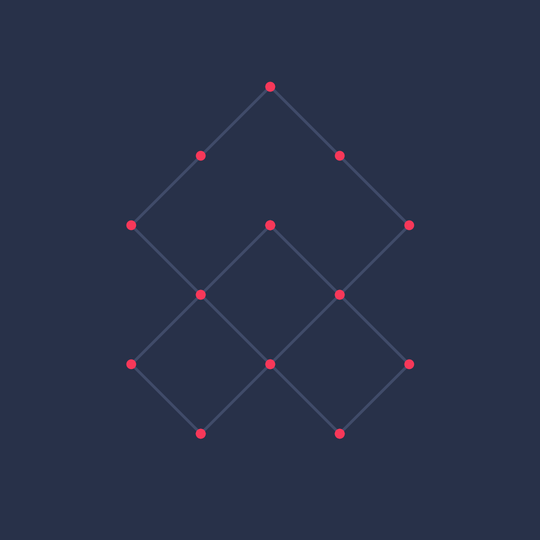
[GIF] Symmetric Minimality (symmetric lattice trefoil knot)

Symmetric lattice trefoil knot

Symmetric Minimality

After I posted Minimal on Mathstodon, David Eppstein asked about and then found a minimal lattice trefoil with 3-hedral symmetry.

Here are the (mean-centered) vertices:

symmetrictrefoil = # - Table[Mean[#], {Length[#]}] &[{{0, 0, 0},
    {1, 0, 0}, {2, 0, 0}, {2, 0, 1}, {2, 1, 1}, {2, 2, 1}, {1, 2, 1}, 
    {0, 2, 1}, {-1, 2, 1}, {-1, 2, 0}, {-1, 2, -1}, {-1, 1, -1}, 
    {0, 1, -1}, {1, 1, -1}, {1, 1, 0}, {1, 1, 1}, {1, 1, 2}, 
    {1, 2, 2}, {1, 3, 2}, {0, 3, 2}, {0, 3, 1}, {0, 3, 0}, {0, 2, 0}, {0, 1, 0}}];

The animation demonstrates the 3-fold symmetry which is lacking from the relatively asymmetric minimal trefoil from Minimal (which was just the one built into KnotPlot).

smootheststep[t_] := -20 t^7 + 70 t^6 - 84 t^5 + 35 t^4;

DynamicModule[{p = {-1, 0, 0}, q = Normalize[{0, 1, 1}], a, b, n, M, pl, θ, 
  cols = RGBColor /@ {"#404b69", "#f73859", "#283149"}},
 Manipulate[
  θ = 2 Pi/3 smootheststep[t];
  {n, b} = RotationMatrix[θ, {-1, -1, 1}].# & /@ {p, q};
  a = Cross[b, n];
  M = {a, b};
  pl = M.# & /@ symmetrictrefoil;
  Graphics[{
    Thickness[.0052], cols[[1]], Line[Append[#, First[#]] &[pl]],
    cols[[2]], Disk[M.#, .05] & /@ Sort[symmetrictrefoil, n.#1 > n.#2 &]},
   ImageSize -> 540, PlotRange -> {{-2.75, 2.75}, {-2.5, 3}}, 
   Background -> cols[[-1]]],
  {t, 0, 1}]
 ]
POSTED BY: Clayton Shonkwiler
3 Replies
Sort By:
J. M.
J. M.
Posted 6 years ago

I modified your code a little bit, but qualitatively it still gives a nice result:

st = AnglePath3D[{-1/2, -3/2, -1/2},
                 {{0, 0}, {0, 0}, {0, -Pi/2}, {Pi/2, 0}, {0, 0}, {0, -Pi/2}, {0, 0},
                  {0, 0}, {Pi/2, 0}, {0, 0}, {0, -Pi/2}, {Pi/2, 0}, {0, 0}, {0, -Pi/2},
                  {0, 0}, {0, 0}, {Pi/2, 0}, {0, 0}, {0, -Pi/2}, {Pi/2, 0}, {0, 0},
                  {0, -Pi/2}, {0, 0}}];

DynamicModule[{p = {-1, 0, 0}, q = Normalize[{0, 1, 1}], b, n, M, pl, 
               cols = RGBColor /@ {"#404b69", "#f73859", "#283149"}},
              Manipulate[{n, b} =
                         {p, q}.RotationMatrix[-2 Pi/3 t^3/(1 - 3 t + 3 t^2),
                                               {-1, -1, 1}];
                         M = Transpose[{Cross[b, n], b}];
                         pl = st.M;
                         Graphics[{{EdgeForm[Directive[Thickness[.0052],
                                                       cols[[1]]]], 
                                    FaceForm[], Polygon[pl]},
                                   {cols[[2]], Disk[#, .05] & /@
                                               (SortBy[st, -n.# &].M)}},
                                   ImageSize -> 540,
                                   PlotRange -> {{-2.75, 2.75}, {-2.5, 3}}, 
                                   Background -> cols[[-1]]], {t, 0, 1}]]
POSTED BY: J. M.

Huh. AnglePath3D[] is a new one to me (in fact, it doesn't even exist on my laptop, which is still on 11.0.1).
POSTED BY: Clayton Shonkwiler

enter image description here - Congratulations! This post is now a Staff Pick as distinguished by a badge on your profile! Thank you, keep it coming, and consider contributing your work to the The Notebook Archive!

POSTED BY: EDITORIAL BOARD
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract