This contribution is an extension of my recent Wolfram Demonstration "Spherical Mirror Anamorphosis of Regular Polygons".

Two questions can be asked when reflecting an object in a spherical (or other) mirror:
- Reflection: how does the (deformed) reflection in a mirror of an object outside the mirror look like?
- Anamorphism: how should a (deformed) object outside the mirror look like in order to be reflected in the mirror as the real object?
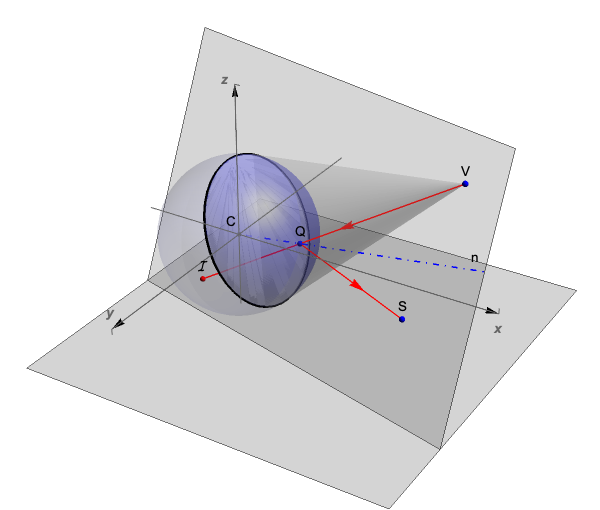
In the spherical mirror centered at C, V is the observer's eye position, S is a (real) point outside the mirror and I is its perceived reflected point inside the mirror. One of the reflected light rays leaving S will meet the mirror at Q such that its reflection meets the eye at V. But the eye at V will now perceive the point S at I. This mirror setup can be used for the computation of both reflection and anamorphism and the points I and S form an "enantiomorphic" pair.
To write the functions that map real points S into reflected points I and vice-versa, we use the law of reflection (ReflectionTransform and EuclideanDistance)
sphericalAnamorphMap[imagePt : {xi_, yi_, zi_}] :=
Module[{solQ, pointQ, reflectionPt, solA},
(*intersection Q of viewline-sphere: Q*)
solQ =(*find the intersection*)
NSolve[{x, y, z} \[Element]
HalfLine[{imagePt, {1*^6, 0, 0}}] && {x, y, z} \[Element]
Sphere[], {x, y, z}];
pointQ = First[{x, y, z} /. solQ];
reflectionPt = ReflectionTransform[pointQ][{-1*^6, 0, 0}];
solA = First@
NSolve[EuclideanDistance[pointQ,
t*(reflectionPt - pointQ) + pointQ ] ==
EuclideanDistance[imagePt, pointQ], t];
(-t*(reflectionPt - pointQ) + pointQ) /. solA]
sphericalReflectionMap[reflectedPt : {xs_, ys_, zs_}] :=
Module[{plane, solQ, pointQ, solI},
plane = InfinitePlane[{{0, 0, 0}, {1*^6, 0, 0}, reflectedPt}];
solQ =(*find the intersection*)
NSolve[{{x, y, z} \[Element] Sphere[], {x, y, z} \[Element] plane,
VectorAngle[reflectedPt - {x, y, z}, {x, y, z}] ==
VectorAngle[{1*^6, 0, 0} - {x, y, z}, {x, y, z}]}, {x, y, z}];
pointQ = Last[{x, y, z} /. solQ];
solI = NSolve[{{x, y, z} \[Element]
HalfLine[{{1*^6, 0, 0}, pointQ}],
EuclideanDistance[{x, y, z}, pointQ] ==
EuclideanDistance[{xs, ys, zs}, pointQ]}, {x, y, z}];
First[{x, y, z} /. solI]]
This shows the two functions to be the inverse of one another: anamorphism as the inverse of reflection
sphericalReflectionMap[sphericalAnamorphMap[{-0.12, -0.1582, -0.112}]]
{-0.12, -0.1582, -0.112}
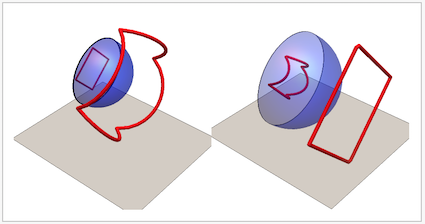
In the "anamorphism" to the left, we see a deformed, anamorphic curve that , when reflected in the mirror is observed as a perfect square.
In the "reflection" to the right we see a perfect square reflected in a spherical mirror and observed as a deformed curve. The left graphics was created using the function sphericalAnamorphMap, the right one using the function sphericalReflectionMap .
It is the first one that is computationally very interesting. It solves e.g. the question: compute a curve which, when reflected in a spherical mirror, will be perceived as a perfect square.
The function sphericalAnamorphMap computes the anamorphic map of a single point. We can now make anamorphic objects as collections of points such as: polygons, polyhedra, graphics primitives and -complexes, tessellated objects from e.g ExampleData[{"Geometry3D",...] or from 3D scanned objects on the www.
The following is a Manipulate that computes the spherical anamorphic map of some regular polygons and a circle.
polygon[\[Theta]_, \[Theta]0_, r_,
n_] :=(*parametric of a regular polygon*)
r Cos[Pi/n] Sec[(2 ArcTan[Cot[(1/2) n (\[Theta] - \[Theta]0)]])/
n] {Cos[\[Theta]], Sin[\[Theta]]}
Manipulate[Module[{polyPts, anamorphPts},
polyPts =
ParallelMap[RotationMatrix[\[Alpha]100, {1, 0, 0}].# &,
ParallelMap[RotationMatrix[\[Alpha]010, {0, 1, 0}].# &,
ParallelMap[RotationMatrix[\[Alpha]001, {0, 0, 1}].# &,
ParallelTable[
polygon[t, .001, r, n], {t, 0,
2 \[Pi], \[Pi]/24}] /. {x_?NumericQ, y_?NumericQ} -> {0, x,
y}]]] /. {x_?NumericQ, y_?NumericQ, z_?NumericQ} -> {x + dx,
y, z};
anamorphPts = Map[sphericalAnamorphMap, polyPts];
Graphics3D[{
{Gray, Opacity[.35],
InfinitePlane[{{0, 0, -2}, {0, 1, -2}, {1, 0, -2}}]},
{(*full sphere*){Opacity[.1], Lighter[Orange, .75], Sphere[]},
(*spherical mirror*)
Style[Sphere[], Specularity[White, 25], Blue, Opacity[.3],
ClipPlanes -> InfinitePlane[{{0, 0, 0}, {0, 1, 0}, {0, 0, 1}}]]},
(*view cone base*){Opacity[.4], EdgeForm@AbsoluteThickness[2],
Cylinder[{{0, 0, 0}, {-.01, 0, 0}}, 1]},
{Red, Tube[polyPts, .025], Tube[anamorphPts, .05]}},
Boxed -> False, PlotRange -> {{-1.5, 4}, {-2, 2}, {-2, 2}},
ViewPoint -> Dynamic@vwp]],
"Geometry", {{r, .7, "Circumradius"}, .25, .988, .01,
ImageSize -> Small}, {{n, 4}, {3, 4, 5, 6, 51 -> "circle"},
SetterBar, Appearance -> "Horizontal" -> {1, 5}}, Delimiter,
"Rotate around", {{\[Alpha]001, .01, "z-axis"}, -\[Pi], \[Pi],
ImageSize -> Small},
{{\[Alpha]010, .01, "y-axis"}, -\[Pi], \[Pi], ImageSize -> Small},
{{\[Alpha]100, .01, "x-axis"}, -\[Pi], \[Pi],
ImageSize -> Small}, Delimiter,
"Move front/back", {{dx, -.4}, -1, 1, .01,
ImageSize -> Small}, Delimiter,
"View direction", {{vwp, {1.3, -2.4, 2},
""}, {{1, -100, 2} -> "sideways",
Right -> "in front", {0, -.05, 100} ->
"from top", {1.3, -2.4, 2} -> "default"}, SetterBar,
Appearance -> "Horizontal" -> {2, 2}}, TrackedSymbols :> True,
SynchronousUpdating -> False]
If we rotate the reflection of a circle around the z-axis (right) or the y-axis (left) and track the anamorphic image, we get this GIF:
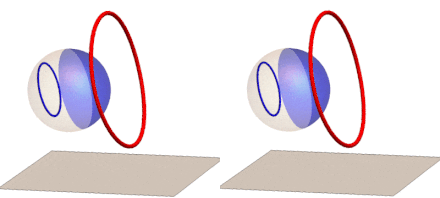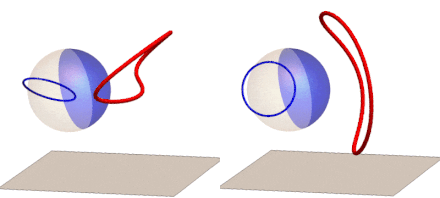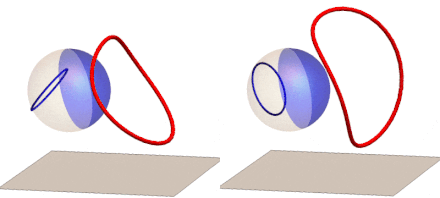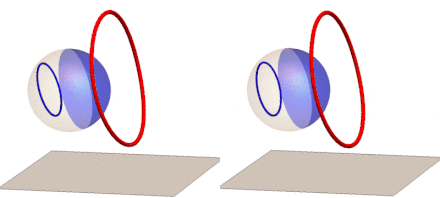
We can now extend our anamorphic imaging to 3D with polyhedron frames:
Manipulate[
Module[{vertices, edges, polyPts, rotatedPts, anamorphPts},
vertices = r*PolyhedronData[pHedron, "Vertices"] // N;
edges = PolyhedronData[pHedron, "Edges"];
polyPts =
ParallelTable[(1 - t) #[[1]] + t #[[2]], {t, 0,
1, .2}] & /@ (Part[vertices, #] & /@ edges);
rotatedPts =
ParallelMap[RotationMatrix[\[Alpha]100, {1, 0, 0}].# &,
ParallelMap[RotationMatrix[\[Alpha]010, {0, 1, 0}].# &,
ParallelMap[RotationMatrix[\[Alpha]001, {0, 0, 1}].# &,
r*polyPts, {2}], {2}], {2}] /. {x_?NumericQ, y_?NumericQ,
z_?NumericQ} -> {x + dx, y, z};
(*anamorphic map of rotated points*)
anamorphPts = Map[sphericalAnamorphMap, rotatedPts, {2}];
Graphics3D[{{Gray, Opacity[.25],
InfinitePlane[{{0, 0, -2}, {0, 1, -2}, {1, 0, -2}}]},
{(*full sphere*){Opacity[.1], Lighter[Orange, .6], Sphere[]},
(*spherical mirror*)
Style[Sphere[], Specularity[White, 25], Gray, Opacity[.4],
ClipPlanes -> InfinitePlane[{{0, 0, 0}, {0, 1, 0}, {0, 0, 1}}]]},
{Red, Tube[#, .02] & /@ rotatedPts, Tube[anamorphPts, .035]}},
Lighting -> {{"Ambient", GrayLevel[0.25]}, {"Directional", White,
ImageScaled[{1, 1, 1}]}},
Axes -> False, Boxed -> False,
PlotRange -> {{-1.25, 4}, {-2, 2}, {-2, 2}}]],
"Polyhedron",
{{pHedron, "Dodecahedron", ""}, {"Cube", "Dodecahedron",
"Icosahedron", "RhombicHexecontahedron"}, SetterBar,
Appearance -> "Horizontal" -> {4, 1}},
{{r, .65, "Circumradius"}, .25, .988, .01,
ImageSize -> Small}, Delimiter,
"Rotate around", {{\[Alpha]001, .1, "z-axis"}, -\[Pi], \[Pi],
ImageSize -> Small},
{{\[Alpha]010, .01, "y-axis"}, -\[Pi], \[Pi], ImageSize -> Small},
{{\[Alpha]100, .01, "x-axis"}, -\[Pi], \[Pi],
ImageSize -> Small}, Delimiter,
"Move front/back", {{dx, -.40}, -1, 1, .01,
ImageSize -> Small}, Delimiter,
SynchronousUpdating -> False]
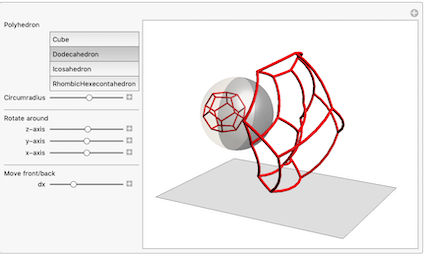
If we rotate the reflection of the cube frame around the z - axis (right) or the y - axis (left) and track the anamorphic image, we get this GIF :
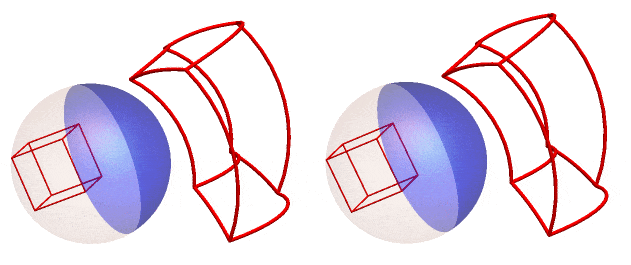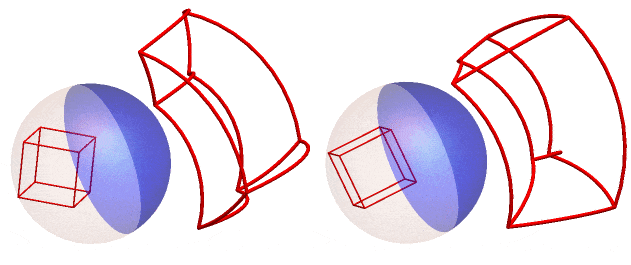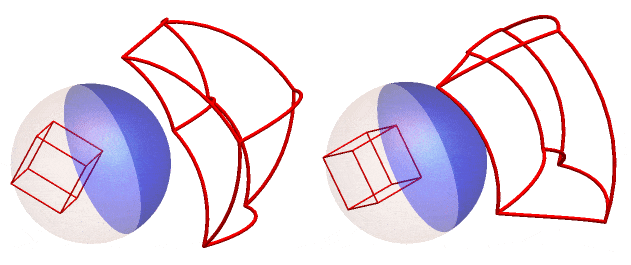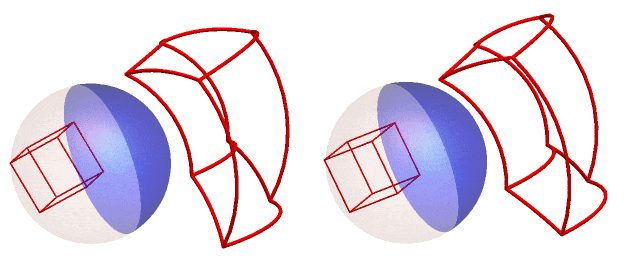
We can also do this for the RhombicHexecontahedron or spikey! (here rotated around the z-axis)

As I did for the cylindrical mirror anamorphosis on my community contribution: Anamorphosis of 3D-Objects & 3D Printing, the mesh of the "Utah Teapot" can also be used after appropriate scaling.
getAndRescale[example_String] :=
Module[{data, ranges, maxRange, temp1, temp2},
data = ExampleData[{"Geometry3D", example}, "PolygonObjects"];
ranges = MinMax@Flatten[data[[All, 1]], 1][[All, #]] & /@ Range[3];
maxRange = MaximalBy[Most@ranges, Abs[Subtract @@ #] &];
temp1 = MapAt[Rescale[#, First@maxRange, {-1, 1}] &,
data, {All, 1, All, 1}];
MapAt[Rescale[#,
Last@ranges, {0,
2*Subtract @@ ranges[[3]]/Subtract @@ ranges[[1]]}] &,
temp1, {All, 1, All, 3}]]
Module[{\[Phi], pts, pts0, offset, ri, data, anaData},
offset = 1/5; ri = Sqrt[1 - offset^2]; \[Phi] = ArcTan[5, 2.5];
(*clippane anchors*)
pts0 = {{offset, 0, 0}, {offset, ri, 0}, {offset, 0, ri}};
pts = RotationMatrix[-\[Phi], {0, 1, 0}].# & /@ pts0;
data = getAndRescale[
"UtahTeapot"] /. {x_?NumericQ, y_?NumericQ,
z_?NumericQ} -> .7 {y - .65, x, z - .5};
anaData =
ParallelMap[(*adapted function sphericalAnamorphMap3D in s"pikey \
gor ptnting.nb" attached*) sphericalAnamorphMap3D[#, {5, 2.5}] &,
data, {3}];
Graphics3D[{
{Gray, Opacity[.25],
InfinitePlane[{{0, 0, -1}, {0, 1, -1}, {1, 0, -1}}]},
{(*spherical mirror*)
Style[Sphere[], Specularity[White, 25], Gray, Opacity[.24],
ClipPlanes -> InfinitePlane[pts]]},
{FaceForm[Lighter[Orange, .85]], EdgeForm[{Thin, Black}], data,
FaceForm[Lighter[Orange, .65]], anaData}, Opacity[.25]},
Boxed -> False]]
These are two perpendicular views of the teapot reflection and its corresponding anamorphic image.
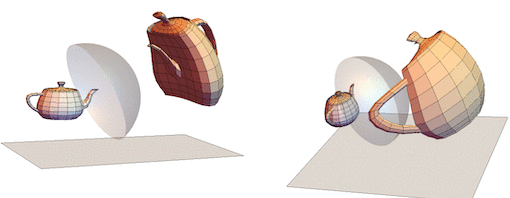
I printed the the right teapot on iMaterialise (STL file "utahTeapot.stl" attached).
teapot = Graphics3D[anaData];
Printout3D[teapot, "utahTeapot.stl", TargetUnits -> "Centimeters",
RegionSize -> 7.25];
Printout3D[teapot, "IMaterialise", TargetUnits -> "Centimeters",
RegionSize -> 7.25]

This is a photo of the printed anamorphic teapot reflected in a 7cm diameter reflective Christmas ball.

Enjoy 3D spherical anamorphism printing.
 Attachments:
Attachments: