Currently public health officials measure ambulance coverage using a simple radius (for urban areas this radius is typically 2.5 miles). However, using a radius to model coverage doesnt give a realistic representation of expected ambulance response times. Modeling coverage using isochrones seems like the most natural fit to accurately measure response times. Isochrones represent all locations that can be travelled to within a certain time limit. In accordance with the Office of the Inspector Generals recommended response times for emergency medical services, we built isochrones of a 5 minute radius. We take an area located on the South Side of Chicago and subdivide it into potential points we can travel to:
NL1 = Subdivide[41.64952897794792`, 41.81247732431524`, 20];
NL2 = Subdivide[-87.71329065894878`, -87.55250871202725`, 20];
grid = Tuples[{NL1, NL2}];
geogrid = Thread[GeoPosition[#] &@grid];
geogridplot = GeoListPlot[geogrid, PlotStyle -> {Lighter@Cyan, Thin},
GeoBackground -> GeoStyling["StreetMapNoLabels",
GeoStylingImageFunction -> (ImageAdjust@Darker@ColorNegate@ColorConvert[#1, "Grayscale"] &)]];
We select the following ambulance location to build an isochrones for:
ambl = GeoPosition[{41.68740625454284`, -87.62413685881735`}];
ambulancesite= GeoListPlot[ambl, PlotStyle -> {Lighter@Red, Thick}];
Show[geogridplot, ambulancesite]

The red point is our ambulance site and the blue points are our grid points.
We start by calculating the distance from our chosen ambulance location to each of the points on our grid using the built in TravelTime[] function:
tt = TravelTime[{ambl, #}] & /@ geogrid;
We send the quantity $Failed to an arbitrary travel time greater than 5 minutes then convert the travel time in minutes to an integer quantity given in seconds.
tt = tt /. {$Failed -> Quantity[100, "Minutes"]};
tt = QuantityMagnitude[UnitConvert[tt]];
Points we cannot travel to within 5 minutes (300 seconds) are coded as 0 and points we can travel to within our time limit are coded as 1.
tt1= tt /. n_Integer /; n < 301 -> 1;
tt0 = tt1 /. n_Integer /; n > 300 -> 0;
coordinates1 = DeleteCases[tt0*grid,0]
coordinates1 only contains points we can reach from our ambulance site within 5 minutes. Now, we want to visualize our isochrones:
isotest = TravelDirections[{ambl, #}] & /@ coordinates1;
GeoGraphics[Style[Line[isotest], Thick, Lighter@Red], {GeoBackground -> GeoStyling["StreetMapNoLabels",
GeoStylingImageFunction -> (ImageAdjust@Darker@ColorNegate@ColorConvert[#1, "Grayscale"] &)]}]
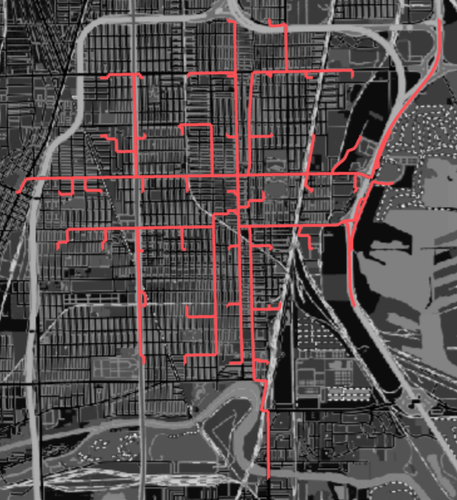
This is a rough approximation of all points we can travel to within 5 minutes from our starting point. We can refine our approximation by taking the CoordinateBound[] of the points from that we can travel to within 320 seconds from our initial travel times-tt-and then subdivide the region to get a new grid of potential points. Here we are allowing ourselves a 20 second error margin to make sure we dont miss any points we can travel to.
ltt = tt /. n_Integer /; n < 321 -> 1;
Ott = ltt /. n_Integer /; n > 320 -> 0;
co320= Ott*grid;
co320 = DeleteCases[co320, {0., 0.}];
CoordinateBounds[co320]
{{41.6495, 41.7147}, {-87.6651, -87.5766}}
Next we create a separate grid to run the TravelTime[] function over:
I1 = Subdivide[41.64952897794792`, 41.71470831649485`, 31];
I2 = Subdivide[-87.66505607487233`, -87.57662600406547`, 31];
IG = Tuples[{I1, I2}];
Subdividing this coordinate bound gives us 1024 points we can travel to within 320 seconds. Now, we run the exact same procedure above to better refine the isochrones:
IG = Thread[GeoPosition[#] &@IG];
itt = TravelTime[{ambl, #}] & /@ IG;
itt= itt /. {$Failed -> Quantity[100, "Minutes"]};
itt = QuantityMagnitude[UnitConvert[itt]];
lit = itt /. n_Integer /; n < 301 -> 1;
Oit = lit /. n_Integer /; n > 300 -> 0;
coordinates2 = Oit*IG;
coordinates2= DeleteCases[coordinates2, 0];
iso = TravelDirections[{ambl, #}] & /@ coordinates2;
Finally we are able to map our improved isochrones and compare the difference in estimating ambulance coverage with a simple radius and isochrones.
GeoGraphics[{{Blue, GeoDisk[ambl, Quantity[2.5, "Miles"]]},
Style[Line[iso], Thick, Lighter@Red]}, {GeoBackground ->
GeoStyling["StreetMapNoLabels",
GeoStylingImageFunction -> (ImageAdjust@
Darker@ColorNegate@ColorConvert[#1, "Grayscale"] &)]}]
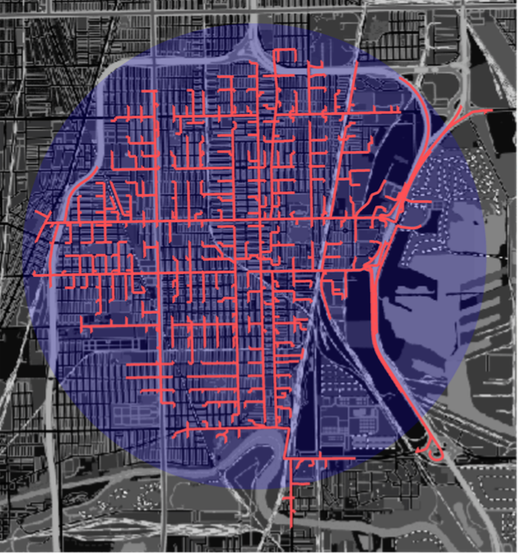
Using a simple radius overestimates coverage in some areas and underestimates coverage in others.