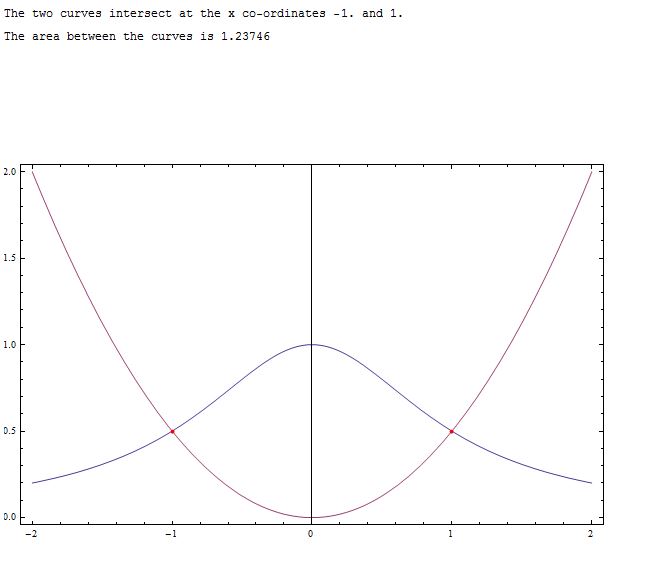
Part 2 looks ok to me
Clear[f, x, g]; {f, g} = {1/(1 + x^2), x^2/
2}; p = {#, f /. x -> #} & /@ (x /. NSolve[f == g, x, Reals]);
p = First /@ p; area = NIntegrate[f - g, {x, p[[1]], p[[2]]}];
Print["The two curves intersect at the x co-ordinates ", p[[1]],
" and ", p[[2]]];
Print["The area between the curves is ", area]; Plot[{f, g}, {x,
p[[1]] - 1, p[[2]] + 1},
Epilog -> {PointSize[0.007],
Red, (Point[{#, f /. x -> #}] &) /@ (x /.
NSolve[f == g, x, Reals])}, ImageSize -> {600, 600},
Frame -> True]