Introduction
You may have noticed that the factorial function for integers generates a lot of trailing zeros at the end e.g. 100! evaluates to
9332621544394415268169923885626670049071596826438162146859296389521759\
9993229915608941463976156518286253697920827223758251185210916864000000\
000000000000000000
That's 24 zeros right there. Maybe you would like to figure out how to calculate the exact number for arbitrary input integers? And then maybe for any chosen radix as well i.e. not using the decimal representation? I don't want to spoil the fun for you, so please go chew away at this nice little mathematical diversion. The asymptotic "TZF" function for large integers is really compute-friendly, so for "easy" large integers you will be able to do the algebra just using a simple rule.
Well and then it is always possible I have made a mistake, so I include my notebook on this problem for you to compare.
Have fun!

In the seventies when I got my first TI pocket calculator in school I developed a certain fascination for the factorial function. It was basically the most dangerous function around because if you entered any integer larger than 69 it would blow up with an error because it could not calculate numbers with more than two digits in the base-10 exponent and for most of them it could of course only show the first few most significant digits.
So it took me almost 40 years and the mind-boggling capacity of WL to handle arbitrary-sized integers (well almost) to ask the following question: What is the number of trailing zeros in $n$ factorial? As a short reminder n! is the mathematical notation for the product of all positive integers less or equal to n.
As you can easily see from an example there are plenty of trailing zeros in the factorial of reasonably-sized integers:
100!
9332621544394415268169923885626670049071596826438162146859296389521759\ 9993229915608941463976156518286253697920827223758251185210916864000000\ 000000000000000000
Well to answer the question above we reformulate it as the number of sought zeros is equal to how many times n factorial can be divided (meaning integer division) by ten without getting a remainder. But for getting a factor of 10 there needs to be a corresponding factor of 5 and one factor of 2 in the prime factorization of $n$ factorial. Since every other number contains at least a factor of 2 in its prime factorization we can safely count only the factors of 5 in the factorization of the first n integers so we get a first (very functional and "pattern matchy" way to calculate the trailing zero function TZF:
TZF1[n_] :=
Flatten[FactorInteger[Range[n]] , 1] // Cases[{5, a_} -> a] // Total
ListPlot[Table[TZF1[n], {n, 100}], Joined -> True, ImageSize -> Large,
PlotRange -> All]
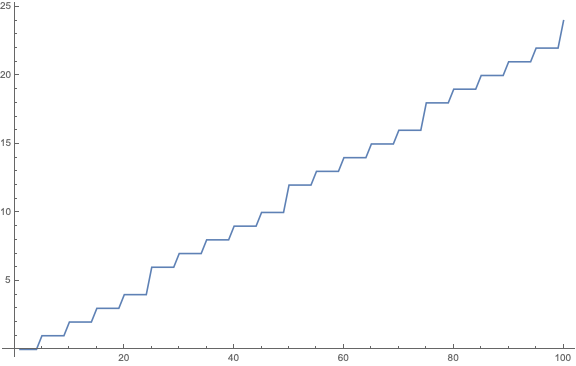
Well it looks pretty step-like with regular intervals so let's plot the differences:
ListPlot[Differences[Table[TZF1[n], {n, 100}]], Joined -> True,
ImageSize -> Large, PlotRange -> All]
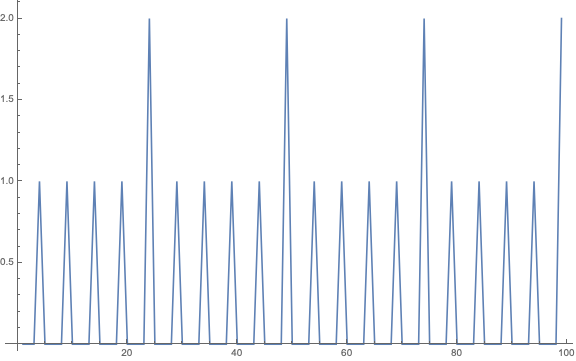
Aha! For each $5^i$ we get i new trailing zeros, but that is then equal to just summing the integer quotients of dividing n by increasing powers of $5^i$. So we have another candidate for the trailing zeros which definitely looks much more procedural:
TZF2[n_] := Module[{i = 1, result = 0}, While[5^i <= n, result += Quotient[n, 5^i]; i++]; result]
And finally we might always have done a mistake so let's just see how long the last group of digits is for any n larger than 4, which is the brute force way to get the answer:
TZF3[n_] := If[n < 5, 0, IntegerDigits[Factorial[n]] // SplitBy[#, 1] & // Part[#, -1] & // Length]
m = 150; ListPlot[{Table[TZF1[n], {n, m}], Table[TZF2[n], {n, m}],
Table[TZF3[n], {n, m}]}, Joined -> True, ImageSize -> Large, PlotRange -> All]
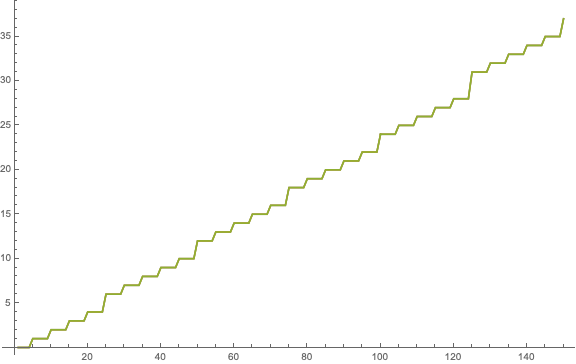
All well it seems, of course not everything worked out right at first trial, but now that all three seem to coincide, it seems pretty watertight right? So then let's see which form might be most efficient to calculate the TZF function:
n = 10000;
Timing[TZF1[n]]
Timing[TZF2[n]]
Timing[TZF3[n]]
{0.041059, 2499}
{0.000055, 2499}
{0.043205, 2499}
So you see functional is not always faster unfortunately, but it is also surprising to see that taking the long detour to calculate the whole factorial does equally well roughly as the first variant which only factorizes rather small numbers.
But back to the original question we can see that we answer the original question pretty accurately by calculating the TZF function divided by n as a geometric sum:
n =.;
Sum[1/5^i, {i, 1, \[Infinity]}]
1/4
So the trailing number of zeros of n factorial is approximately $n/4$ for large n (to be more accurate take one less). So if you get the question at the next party "how many trailing zeros are there in 10000 factorial?" just say "2499 of course"!
So what about other radices (plural for radix or base of the integer digit representation)? To find an the answer we have to consider the prime factorization of the radix which then of course can have more (or less) than two prime factors and each with a separate multiplicity to form the radix as a product. So for each of these prime factors of the radix $p^k$ we then have to calculate how many times p appears in the positive integer numbers smaller or equal to n and find the integer quotient when dividing by k. The smallest of these is then our trailing zeros count.
TZF4[n_, r_] := Quotient[Total[ Cases[Flatten[FactorInteger[Range[n]] , 1] , {#[[1]], a_} ->
a]], #[[2]]] & /@ FactorInteger[r] // Min
TZF5[n_, r_] :=
Module[{f = FactorInteger[r], q = Table[0, Length[FactorInteger[r]]],
i, p, q0},
Do[i = 1; p = f[[j, 1]]; q0 = 0;
While[p^i <= n, q0 += Quotient[n, p^i]; i++];
q[[j]] = q0
, {j, Length[f]}];
If[Min[q] > 0, Min[Quotient[q, f[[;; , 2]]]], 0]
]
TZF6[n_, r_] :=
IntegerDigits[Factorial[n], r] // SplitBy[#, 1] & //
If[Part[#, -1][[1]] == 0, Length[Part[#, -1]], 0] &
Let's see if these agree to iron out obvious mistakes by feeding random samples. But beware, the factorial is still dangerous and will exhaust your physical memory if you throw in too big numbers or too small radices.
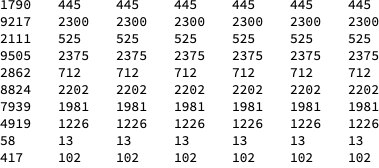
Table[{n = RandomInteger[10000], r = RandomInteger[{5, 30}],
TZF4[n, r], TZF5[n, r], TZF6[n, r]}, 10] // TableForm
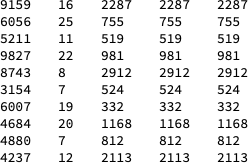
Table[{n = RandomInteger[10000], TZF1[n], TZF2[n], TZF3[n],
TZF4[n, 10], TZF5[n, 10], TZF6[n, 10]}, 10] // TableForm
In order to get asymptotic values of the trailing zeros you now need to divide n by $(p-1) k$. You have to do this only with the prime factor that results in the largest value of $(p-1) k$ of course. Then you round down again and you will be mostly very accurate. So let's do an example:
TZF5[10000, 72]
2498
For radix 72 the prime decomposition is $2^3 3^2$, so again it's a division by four (from the first factor) but now we'd actually would have to subtract 2 to get the right number. If you end up with a tricky radix decomposition for the party trick you might actually have to consult the pocket calculator on your smartphone for the division. To close out I have to confess that I still own a working HP-15C, an icon of computation devices and a testament to solid engineering:
Well I am looking forward to the day when we are going to have hardware that durable again and being able to run WL from it.
If you liked this piece and want to explore further, why not generalizing the TZF functions above to mixed radix representations or make your own variant of them to optimize code, memory or performance.

 Attachments:
Attachments: