Hi Ed,
I can confirm this. V11.3 is a bit faster, but both 11.3 and 12 produce the unstable response. It is clearly an error.
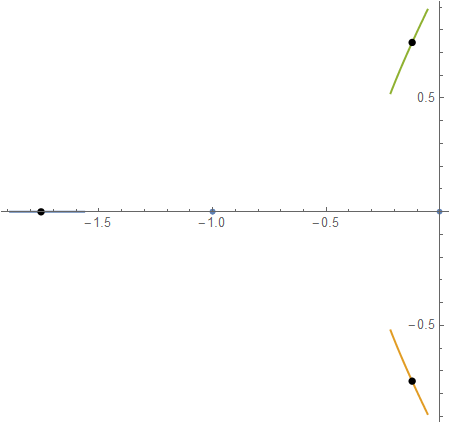
RootLocusPlot confirms the system is stable with k=1:
tfm = TransferFunctionModel[k 1/(s (s + 1)^2 + k), s];
RootLocusPlot[tfm, {k, .5, 1.5}, FeedbackType -> None,
PoleZeroMarkers -> {None, Automatic, None, "ParameterValues" -> {1}}]
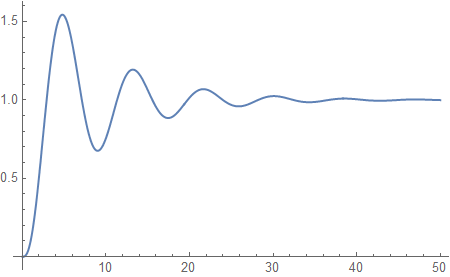
Using Laplace transforms gives a believable result:
stepResponse = InverseLaplaceTransform[k 1/(s (s + 1)^2 + k)/s, s, t];
Plot[stepResponse /. k -> 1, {t, 0, 50}, PlotRange -> All]
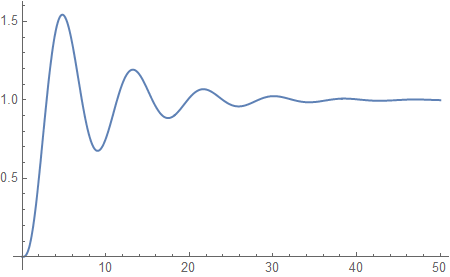
And so does OutputResponse for the model with k = 1:
out = OutputResponse[tfm /. k -> 1, UnitStep[t], {t, 0, 50}];
Plot[out, {t, 0, 50}, PlotRange -> All]
I have reported three issues regarding Control Systems so far. Two have been confirmed as bugs. The third involved numerical instability in OutputResponse, for which I have had no reply.
I suggest you report this to Tech Support.
Kind regards,
David