Hi David

Many thanks for the examples. Thanks to one of them, I wrote an animation that works in this case.

Manipulate[
 tfm = TransferFunctionModel[k 1/(s (s + 1)^2 + k), s];
 out = OutputResponse[tfm /. k -> kval, UnitStep[t], {t, 0, 50}];
 Plot[out, {t, 0, 50}, PlotRange -> All],
 {{kval, 1, "Gain"}, 0, 100, 1, Appearance -> "Labeled"}]

I have been reporting Control Toolbox bugs since the time one had to buy it separately (Control System Professional version 2.1). I think this issue will be another one on my list.

Kind Regards

Ed

Hi Ed,

I can confirm this. V11.3 is a bit faster, but both 11.3 and 12 produce the unstable response. It is clearly an error.

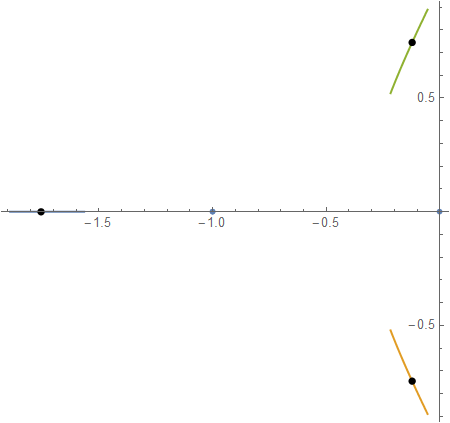
RootLocusPlot confirms the system is stable with k=1:

tfm = TransferFunctionModel[k 1/(s (s + 1)^2 + k), s];

RootLocusPlot[tfm, {k, .5, 1.5}, FeedbackType -> None, 
 PoleZeroMarkers -> {None, Automatic, None, "ParameterValues" -> {1}}]

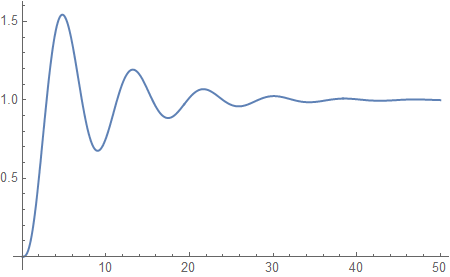
Using Laplace transforms gives a believable result:

stepResponse = InverseLaplaceTransform[k 1/(s (s + 1)^2 + k)/s, s, t];

Plot[stepResponse /. k -> 1, {t, 0, 50}, PlotRange -> All]

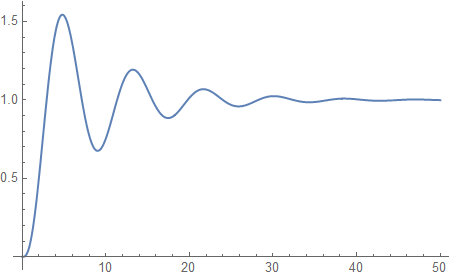
And so does OutputResponse for the model with k = 1:

out = OutputResponse[tfm /. k -> 1, UnitStep[t], {t, 0, 50}];
Plot[out, {t, 0, 50}, PlotRange -> All]

I have reported three issues regarding Control Systems so far. Two have been confirmed as bugs. The third involved numerical instability in OutputResponse, for which I have had no reply.

I suggest you report this to Tech Support.

Kind regards,

David