Message Boards Message Boards

0
|
5983 Views
|
6 Replies
|
7 Total Likes
View groups...
Share
Share this post:

[?] Solve equation t + Sin[w t] = a in t?

Ermanno Citraro
Posted 5 years ago

Hi,

Is there a way to solve (also in an approximate way) an equation of this type with Mathematica?

t + Sin[w t] = a in variable t.

Using Solve[t + Sin[w t] == a, t] can't get the solution.

Thanks!
POSTED BY: Ermanno Citraro
6 Replies
Sort By: 
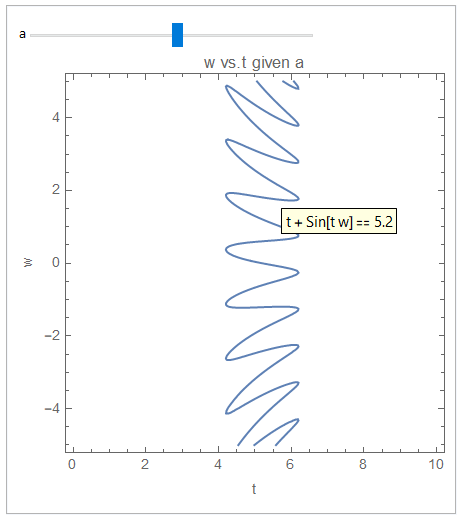
DynamicModule[{k}, Panel[
  Column[{
    Row[{"a", " ", Slider[Dynamic[k], {1, 9, 0.3}]}], 
    With[{a = k}, 
     Dynamic@ContourPlot[t + Sin[w t] == a, {t, 0, 10}, {w, -5, 5}, 
       PlotPoints -> 25, ImageSize -> 300, 
       PlotLabel -> "w vs.t given a", FrameLabel -> {"t", "w"}
       ]]}]
  ]
 ]

sweeping
POSTED BY: Shenghui Yang

Very nice, didn't know this feature!
POSTED BY: Ermanno Citraro

Closely related to Kepler's Equation.
POSTED BY: John Doty

Interesting:)
POSTED BY: Ermanno Citraro

Thanks!
POSTED BY: Ermanno Citraro

General analytical solution for transcendental equation is impossible.

Approximation by numerics: 

     w = 1; a = 1;

     sol = Solve[t + Sin[w t] == a, t, Reals];
     sol // N;
     (*{{t -> 0.510973}} *)

     sol2 = NSolve[t + Sin[w t] == a && -10 < t < 10, t, Reals]
     (*{{t -> 0.510973}} *)

     sol3 = FindRoot[t + Sin[w t] == a, {t, 1}]
     (*{t -> 0.510973}*)

Regards M.I.
POSTED BY: Mariusz Iwaniuk
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract