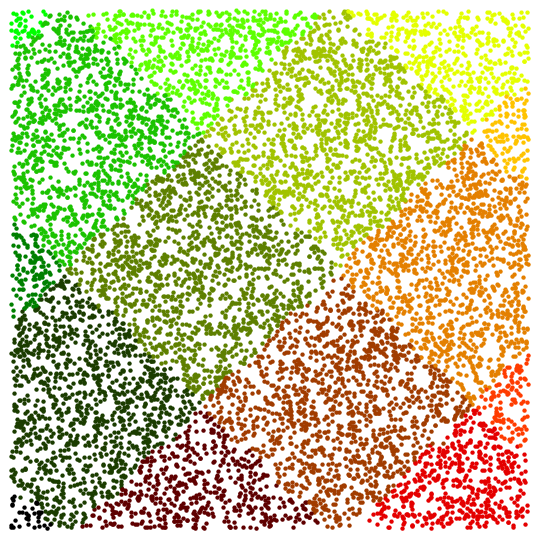
Thanks for the code, it is interesting to compare different methods. For example, if one changes the default
"StepControl" -> "LineSearch" to
"StepControl" -> "TrustRegion", the plot becomes well-ordered:
n = 10^4; SeedRandom[0];
rs = RandomReal[{-6, 6}, {n, 2}];
Off[FindArgMin::lstol];
resn = FindArgMin[Sin[x] Cos[y], Thread[{{x, y}, #}],
Method -> {"Newton", "StepControl" -> "TrustRegion"}] & /@ rs;
c[{x_, y_}] = RGBColor[(x + 6)/12, (y + 6)/12, 0]; Show[
Graphics@Table[{c[resn[[i]]], Point[rs[[i]]]}, {i, n}]]
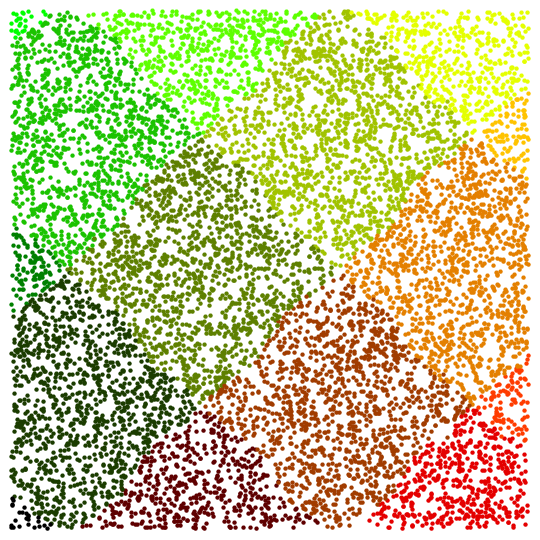
From the other side, setting bigger value of
"StartingScaledStepSize" suboption gives lesser ordered result as expected:
n = 10^4; SeedRandom[0];
rs = RandomReal[{-6, 6}, {n, 2}];
Off[FindArgMin::lstol];
resn = FindArgMin[Sin[x] Cos[y], Thread[{{x, y}, #}],
Method -> {"Newton",
"StepControl" -> {"TrustRegion",
"StartingScaledStepSize" -> 10}}] & /@ rs;
c[{x_, y_}] = RGBColor[(x + 6)/12, (y + 6)/12, 0]; Show[
Graphics@Table[{c[resn[[i]]], Point[rs[[i]]]}, {i, n}]]
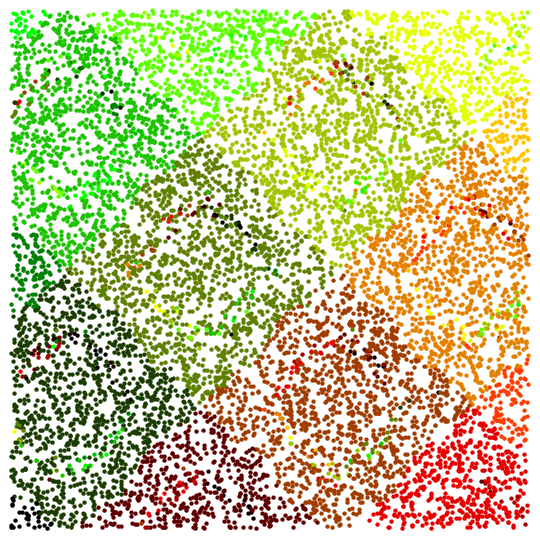
There also are
other suboptions of the "TrustRegion" method one can play with.
And playing with the
"StepControl" -> "LineSearch" suboptions allows to get well-ordered result too:
n = 10^4; SeedRandom[0];
rs = RandomReal[{-6, 6}, {n, 2}];
Off[FindArgMin::lstol];
resn = FindArgMin[Sin[x] Cos[y], Thread[{{x, y}, #}],
Method -> {"Newton",
"StepControl" -> {"LineSearch",
"MaxRelativeStepSize" -> .1}}] & /@ rs;
c[{x_, y_}] = RGBColor[(x + 6)/12, (y + 6)/12, 0]; Show[
Graphics@Table[{c[resn[[i]]], Point[rs[[i]]]}, {i, n}]]