It started in India(left) and was adapted in Iceland (mid). Now you can see it as experiments in several villages in Holland and Belgium(right). They are called 3D crosswalks and are part of a new trend in traffic safety called "nudging" or helping drivers become more aware of dangerous situations by small indirect suggestions.

This visual illusion of "floating blocks" are a perfect example of perspective anamorphism. We can use Mathematica to visualize and make a template to paint this new, and allegedly safer, type of crosswalk.
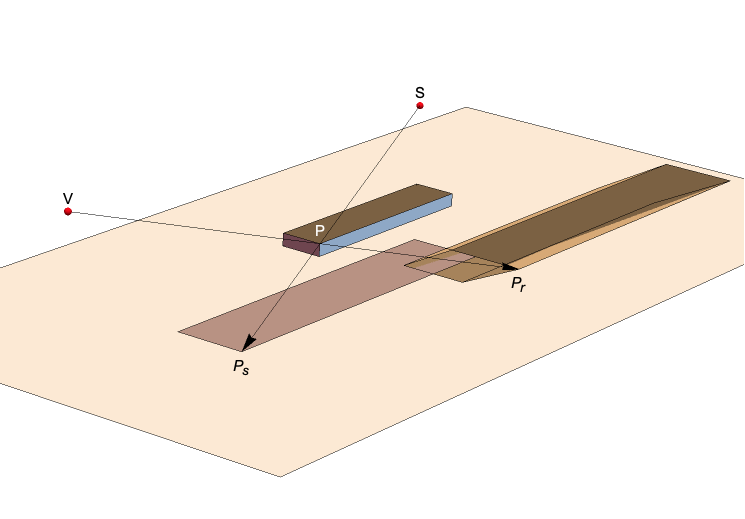
P is a vertex of one of the 3D roadblock cuboids. We are interested in two projections of P to the street level (the z==0 plane): Pr starting from the driver's view point V and Ps (the shadow), starting form the sun S or light source. We do this for all the vertices of the road blocks and we convert a set of 3D primitives into a 2D graphics of the blocks and their shadow that can be painted on the street.
This function computes the projection a point pt from the viewPt to the plane z==0 .
project[pt_List, viewPt : {xv_, yv_, zv_}] :=
Module[{base, viewLine},
base = InfinitePlane[{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}}];
viewLine = HalfLine[{viewPt, pt}];
NSolve[{x, y, z} \[Element] viewLine && {x, y, z} \[Element]
base, {x, y, z}][[1, All, -1]]]
This Manipulate makes all these computations for a whole set of parameters. You can use it to make a template for making your own crosswalk proposal and maybe make your neighborhood street more safe for pedestrians?!
Manipulate[
Module[{stripeWidth, step, viewPt, sun, road, fronts, tops, lefts,
rights, shadow},
step = 51/(n - 1); stripeWidth = sFr step; viewPt = {vx, -vy, vz};
sun = {sx, sy, sz};
road = InfinitePlane[{{0, 0, -.01}, {1, 0, -.01}, {0, 1, -.01}}];
fronts = ParallelTable[{{p, 5, sH}, {stripeWidth + p, 5,
sH}, {stripeWidth + p, 5, sH + sTh}, {p, 5, sH + sTh}}, {p,
Range[0, 51, step]}];
tops = ParallelTable[{{stripeWidth + p, 5, sTh + sH}, {p, 5,
sTh + sH}, {p, 5 + sL, sTh + sH}, {stripeWidth + p, 5 + sL,
sTh + sH}}, {p, Range[0, 51, step]}];
lefts = ParallelTable[{{p, 5, sH}, {p, 5, sTh + sH}, {p, 5 + sL,
sTh + sH}, {p, 5 + sL, sH}}, {p, Range[0, 51, step]}];
rights = ParallelTable[{{stripeWidth + p, 5, sH}, {stripeWidth + p,
5, sTh + sH}, {stripeWidth + p, 5 + sL,
sTh + sH}, {stripeWidth + p, 5 + sL, sH}}, {p,
Range[0, 51, step]}];
shadow = ParallelMap[project[#1, sun] &, tops, {2}];
Column[{Graphics3D[{{Gray, road}, {Red,
Ball[viewPt, .1]}, {Lighter[Black, .05],
Polygon /@ shadow}, {{Lighter[Gray, .55],
ParallelMap[Polygon, lefts]}, {Lighter[Gray, .55],
ParallelMap[Polygon, rights]}, {White,
ParallelMap[Polygon, tops]}, {Lighter[Black, .35],
ParallelMap[Polygon, fronts]}}, {White, AbsoluteThickness[6],
Line[{{-2, -10, 0}, {-2, 40, 0}}],
Line[{{n step, -10, 0}, {n step, 40, 0}}]}}, Boxed -> False,
ViewCenter -> {{0.5`, 0.5`, 0.5`}, {0.5`, 0.734}},
ViewPoint -> .75 {0., -5, 1.},
PlotRange -> {Automatic, {-10, 40}, Automatic},
Lighting -> {{"Ambient", White}}, ImageSize -> {550, 200},
PlotLabel ->
Style["3D: what an approaching driver sees", 15, Bold]],
Graphics[{{Black, Polygon /@ shadow}, {Lighter[Gray, 0.5`],
Polygon[ParallelMap[project[#1, viewPt] &,
rights, {2}]]}, {Lighter[Gray, .75],
Polygon[ParallelMap[project[#1, viewPt] &,
lefts, {2}]]}, {White,
Polygon[ParallelMap[project[#1, viewPt] &,
tops, {2}]]}, {Lighter[Black, .35],
Polygon[ParallelMap[project[#1, viewPt] &,
fronts, {2}]]}} /. {x_?NumericQ, y_, z_} :> {x, y},
Background -> Gray, ImageSize -> 550,
PlotLabel ->
Style["2D: what is painted on the road", White, 15, Bold]]}]],
Style["driver view position", Bold], {{vx, 27, "view pos-x"},
None}, {{vy, 25, "view distance"}, 1, 50, 1,
Appearance -> "Labeled",
ImageSize -> Small}, {{vz, 15, "view height"}, 10, 25, 1,
Appearance -> "Labeled", ImageSize -> Small}, Delimiter,
Style["sun position (for shadows)",
Bold], {{sy, 50, 1, "sun distance"},
None}, {{sx, 28., "direction"}, -50, 150, 1,
Appearance -> "Labeled", ImageSize -> Small}, {{sz, 350, "height"},
200, 1000, 5, Appearance -> "Labeled",
ImageSize -> Small}, Delimiter,
Style["stripes specification", Bold], {{n, 11, "number of stripes"},
Range[6, 15]}, {{sFr, .65, "width as fraction of step"},
Range[.5, .75, .05]}, {{sH, 2., "height above road"}, .01, 5, .01,
Appearance -> "Labeled", ImageSize -> Small}, {{sL, 16, "lenght"},
5, 20, .1, Appearance -> "Labeled",
ImageSize -> Small}, {{sTh, 1.25, "thickness"}, .5, 2.5, .01,
Appearance -> "Labeled", ImageSize -> Small}]
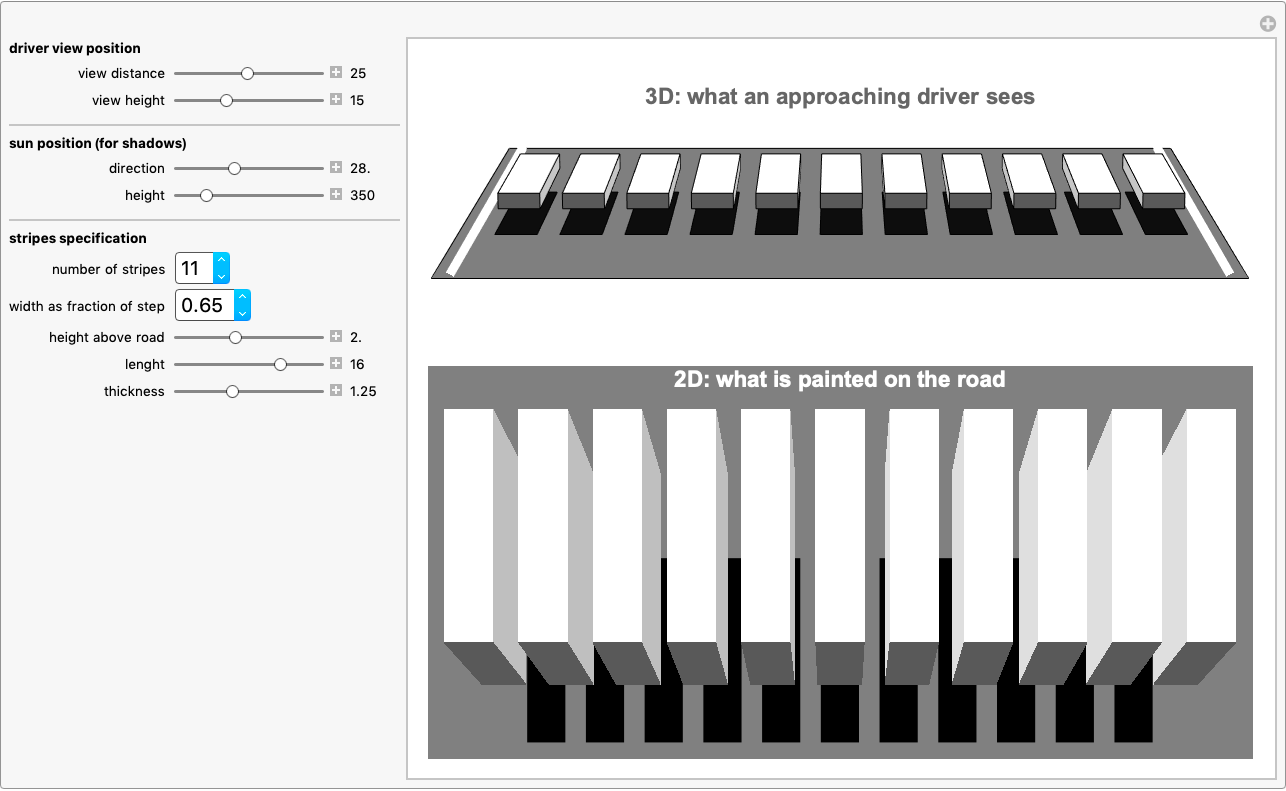
I could not paint a printout on the street in my home town but I printed a smaller version on paper (right), put in on my desktop and simulated what a car driver would see (left) looking at the "crosswalk".
