I'm working with a system of partial differential equations with Mathematica--the two linearized momentum equations below--and I'm having trouble figuring out how exactly to solve them.
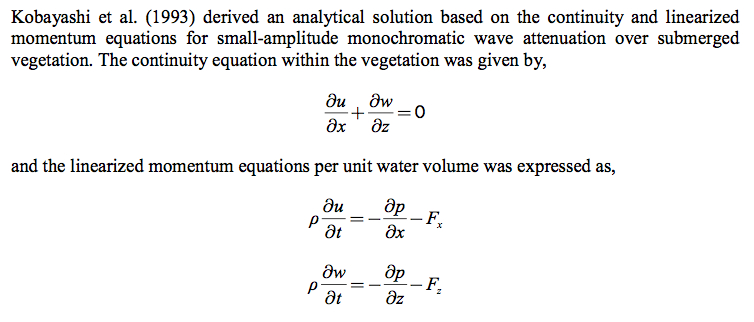
I've tried using DSolve and NDSolve, but I keep running into errors. u and w (velocities) are functions of [t,x] and [t,z] respectively. The problem I'm getting is that Fx, Fz, and p include powers of u and w terms in their definitions and DSolve and NDSolve don't seem to like that. The following definitions are straight from the above paper, consider just the u and x equation:
Fx:=(\[Rho]*B*Cx*u[t,x]*Abs[u[t,x]])/2
Cx:=0.4+(4600/Renx)^2.9
Ren:=(u[t,x]*L)/v
p:=(\[Rho]*u[t,x]^2)/2
Where Rho, B, L, and v are constants:
\[Rho]:=1000
B:=200
L:=.019
v:=1.005*10^-6
Is there a better way to solve this? Ideally I'd like to include the boundary conditions:
u[t,0]==t
u[0,x]==1.3*E^(x)
I've tried to find advice online and in person, but I've been unsuccessful. Any advice or code would be wicked much appreciated!