This post is part of a set of posts related to the general project of Fact Validation that I was working on during the 2019 Wolfram Summer School. This link takes you back to the general overview of the series Fact Validation

Introduction

Syntactic structures for sentences and utterances are very specific instances of linguistic theory applied to concrete sentences or utterances. These constituent tree structures do not just reflect some theoretically motivated assumptions about how words group in sentences and how word order is established in a particular language. They in fact express semantic properties and relations between elements in the clause. Consider the sentence "She saw the man with binoculars."

TextStructure["She saw the man with binoculars.", 
   "ConstituentGraphs"][[1]]

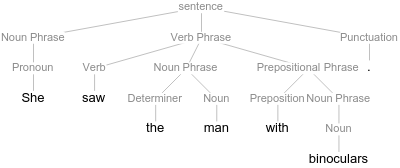
The TextStructure function generated a syntactic tree that indicates that the Prepositional Phrase "with binoculars" is attached to the Verb Phrase. Semantically this implies that the binoculars were an instrument that semantically modifies the action denoted by the predicate. She used the binoculars to see the man somewhere in a distance, for example. The sentence, however, is ambiguous. It can also have a reading where the man for example was holding binoculars in the hand, where the binoculars were a property or modification of the man. This interpretation is expressed in the following constituent tree:

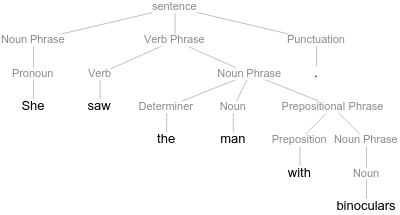
Sentences that have multiple readings are called ambiguous. Without additional context we cannot disambiguate the sentence and pick one reading. We might have a preferred reading, and in fact such a preferred reading might be language or dialect specific. In cases where such ambiguities are expressed in terms of different syntactic structures or constituent trees, where for example certain phrases are attached high to the Verb Phrase or to the direct object Noun Phrase, we talk about structural ambiguity. We express certain kind of ambiguities using constituent trees and variation in terms of attachment and hierarchy of nodes and phrases.

In the first tree above the Prepositional Phrase has scope over the Verb Phrase and thus modifies the semantic properties of it. In the second constituent tree the Prepositional Phrase has scope over the direct object Noun Phrase and modifies its semantic properties. Scope in such trees can be understood as the sub-tree that is contained under the node that contains the particular phrase.

Depending on the application, we might be interested in knowing that a particular sentence is ambiguous. In other applications we might be interested in ways to find the most likely constituent tree, that is we might want to disambiguate sentences using for example context or additional information.

The Scope of Negation

Another kind of structural property that is highly relevant when we analyze text is negation. Identifying and processing the scope of negation is challenging, but absolutely important when processing unstructured text and linguistic information in general.

A very common approach seems to be to just treat a sentence as a bag of words and look for the existance of "not" in it. Alternatively, one could compute the average vector over all sentence words using word embeddings, resulting in an classifier that detects negation of some type in text. These shallow methods are not able to differentiate between the two sentences:

John Smith did not meet the president, but ...

John Smith did meet not the president, but ...

The first sentence denies that there was an event of "meeting the president" that John Smith was subject of (or to). The second sentence does not denie the fact that "John Smith met somebody," it just denies the fact that it was "the president" who he met. For the first sentence we describe the negation as having global scope, that is, it denies the predicate and thus the entire proposition. In the second case we assume that the negation has local scope, that is, that it denies the Noun Phrase "the president" as being a valid object of the predicate "meet" in this sentence.

Consider the hierarchical relations of constituents in a sentence like "John Smith does not love Mary Jones." as given in the following tree:

TextStructure["John Smith does not love Mary Jones.", 
  "ConstituentGraphs"][[1]]

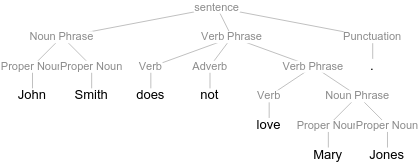
The Negation in this case is labeled as Adverb and in fact hierarchically directly subsumed under the Verb Phrase node. This structural position indicates that the negation operator denies the truth value of the proposition, it in fact is a sentential negation that does not deny the existence of John Smith or Mary Jones, just the relation between them that the main predicate denotes.

Since negation is a special element that can be applied to various kinds of linguistic elements, constituents, or phrases, I prefer to name it as such, simply Negation, as in the following tree:

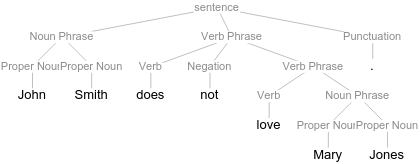
Assume that our constituent trees correctly identify negation as a special element that is not comparable to common adverbs or other modifiers, we can now look at the constituent parse tree that is assigned by our grammar and parser to the sentence "John Smith loves not Mary Jones, but Susan Peters.":

TextStructure["John Smith loves not Mary Jones, but Susan Peters.", 
  "ConstituentGraphs"][[1]]

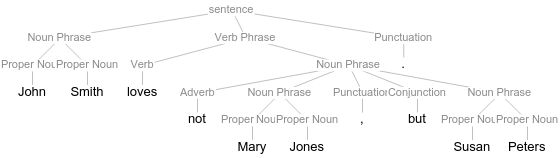
The parser generated a constituent structure that is slightly wrong, by attaching negation to the conjoined Noun Phrase "Mary Jones" and "Susan Peters." Semantically only "Mary Jones" is in the scope of negation. Thus this corrected and relabeled tree is more adequately reflecting the semantic properties of the sentence:

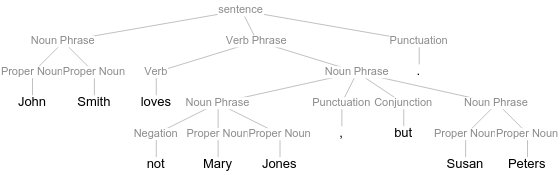
Assume that our parser is capable of generating constituent trees of this kind, that more adequately describe the semantic properties of the underlying sentence, we can try to identify computationally the attachment node of the Negation projection and compute the elements in scope of it.

The constituent trees above are defined as Graph instances in Wolfram Language. Assume that the Graph definition of the constituent tree for the sentence above is defined as follows (some less relevant elements of the Graph are left out):

g1 = Graph[{"ProperNoun1", "John1", "ProperNoun2", "Smith1", "NounPhrase1",
   "Verb1", "loves1", "Negation1", "not1", "ProperNoun3", "Mary1", 
  "ProperNoun4", "Jones1", "NounPhrase3", "Punctuation1", ",1", 
  "Conjunction1", "but1", "ProperNoun5", "Susan1", "ProperNoun6", 
  "Peters1", "NounPhrase4", "NounPhrase2", "VerbPhrase1", 
  "Punctuation2", ".1", 
  "Sentence1"}, {"ProperNoun1" \[UndirectedEdge] "John1", 
  "ProperNoun2" \[UndirectedEdge] "Smith1", 
  "NounPhrase1" \[UndirectedEdge] "ProperNoun1", 
  "NounPhrase1" \[UndirectedEdge] "ProperNoun2", 
  "Verb1" \[UndirectedEdge] "loves1", 
  "Negation1" \[UndirectedEdge] "not1", 
  "ProperNoun3" \[UndirectedEdge] "Mary1", 
  "ProperNoun4" \[UndirectedEdge] "Jones1", 
  "NounPhrase3" \[UndirectedEdge] "ProperNoun3", 
  "NounPhrase3" \[UndirectedEdge] "ProperNoun4", 
  "Punctuation1" \[UndirectedEdge] ",1", 
  "Conjunction1" \[UndirectedEdge] "but1", 
  "ProperNoun5" \[UndirectedEdge] "Susan1", 
  "ProperNoun6" \[UndirectedEdge] "Peters1", 
  "NounPhrase4" \[UndirectedEdge] "ProperNoun5", 
  "NounPhrase4" \[UndirectedEdge] "ProperNoun6", 
  "NounPhrase3" \[UndirectedEdge] "Negation1", 
  "NounPhrase2" \[UndirectedEdge] "NounPhrase3", 
  "NounPhrase2" \[UndirectedEdge] "Punctuation1", 
  "NounPhrase2" \[UndirectedEdge] "Conjunction1", 
  "NounPhrase2" \[UndirectedEdge] "NounPhrase4", 
  "VerbPhrase1" \[UndirectedEdge] "Verb1", 
  "VerbPhrase1" \[UndirectedEdge] "NounPhrase2", 
  "Punctuation2" \[UndirectedEdge] ".1", 
  "Sentence1" \[UndirectedEdge] "NounPhrase1", 
  "Sentence1" \[UndirectedEdge] "VerbPhrase1", 
  "Sentence1" \[UndirectedEdge] "Punctuation2"},
    ... ]

The graph definition exposes the definition of nodes as a concatenation of part-of-speech or category labels and a unique enumerator. This is a necessary way to provide unique labels for all node. As mentioned above, here the labeling of the nodes deviates from the default labels in Wolfram Language. The Negation node is introduced to simplify the identification of the negation terminal in the constituent tree, and as mentioned, the specific label Negation reflects much better the unique status of negation in natural language.

Given this Graph data structure in g1, we can now identify the positions of all Negation nodes in the tree:

negPositions = Flatten[Position[If[StringMatchQ[#[[2]], StartOfString ~~ "Negation" ~~ __], "Neg", "-"] & /@ EdgeList[ g1 ], "Neg"]]

In our case this will return the following list (stored in the variable negPositions):

{17}

This means there is only one Negation node at position 17. We can extract the list of nodes that is directly dominating the Negation nodes as follows:

Take[#[[1]] & /@ EdgeList[ g1 ], # & /@ negPositions ]

This will return us the list of nodes that directly dominate each of the negations in the negPositions list, which is in our case:

{NounPhrase3}

We can remove the unique enumerator from the name and directly decide whether the Negation node has scope over a local phrase like NounPhrase or PrepositionalPhrase, or global scope over the VerbPhrase:

Take[StringDelete[#[[1]], DigitCharacter .. ] & /@ 
  EdgeList[ g1 ], # & /@ negPositions ]

This results in a list of only dominating node category labels, which might provide sufficient information for decisions in specific applications:

{NounPhrase}

Let us consider for validation purposes the graph for the case where the negation is a true sentential negation with global scope, that is, where the Negation node is attached to the Verb Phrase node (again, this Graph is simplified, that is the style elements are removed):

g2 = Graph[{"ProperNoun1", "John1", "ProperNoun2", "Smith1", 
   "NounPhrase1", "Verb1", "does1", "Negation1", "not1", "Verb2", 
   "love1", "ProperNoun3", "Mary1", "ProperNoun4", "Jones1", 
   "NounPhrase2", "VerbPhrase2", "VerbPhrase1", "Punctuation1", ".1", 
   "Sentence1"}, {"ProperNoun1" \[UndirectedEdge] "John1", 
   "ProperNoun2" \[UndirectedEdge] "Smith1", 
   "NounPhrase1" \[UndirectedEdge] "ProperNoun1", 
   "NounPhrase1" \[UndirectedEdge] "ProperNoun2", 
   "Verb1" \[UndirectedEdge] "does1", 
   "Negation1" \[UndirectedEdge] "not1", 
   "Verb2" \[UndirectedEdge] "love1", 
   "ProperNoun3" \[UndirectedEdge] "Mary1", 
   "ProperNoun4" \[UndirectedEdge] "Jones1", 
   "NounPhrase2" \[UndirectedEdge] "ProperNoun3", 
   "NounPhrase2" \[UndirectedEdge] "ProperNoun4", 
   "VerbPhrase2" \[UndirectedEdge] "Verb2", 
   "VerbPhrase2" \[UndirectedEdge] "NounPhrase2", 
   "VerbPhrase1" \[UndirectedEdge] "Verb1", 
   "VerbPhrase1" \[UndirectedEdge] "Negation1", 
   "VerbPhrase1" \[UndirectedEdge] "VerbPhrase2", 
   "Punctuation1" \[UndirectedEdge] ".1", 
   "Sentence1" \[UndirectedEdge] "NounPhrase1", 
   "Sentence1" \[UndirectedEdge] "VerbPhrase1", 
   "Sentence1" \[UndirectedEdge] "Punctuation1"},
    ... ]

Given the Graph definition in g2, the position of the only negation in the sentence can be computed using:

Flatten[Position[
   If[StringMatchQ[#[[2]], StartOfString ~~ "Negation" ~~ __], "Neg", 
      "-"] & /@ EdgeList[ g2 ], "Neg"]][[1]]

This will return:

15

The corresponding scopal node in the constituent tree is then:

Take[ StringDelete[#[[1]], DigitCharacter..]& /@ EdgeList[ g2 ], # & /@ Flatten[ Position[ If[ StringMatchQ[#[[2]], StartOfString ~~ "Negation" ~~ __ ], "Neg", "-" ] & /@ EdgeList[ g2 ], "Neg" ]]][[1]]

This outputs:

VerbPhrase

This very simple approach allows us now to quickly extract the scope relations of the negation or other quantifiers and operators from constituent parse trees.

Summary

To conclude, this short excursion into NLP and linguistic analysis shows us that it is important to utilize existing linguistic outputs like constituent parse trees for advanced semantic processing of natural language utterances. We might be interested in detecting ambiguities in sentences, the correct scope of the negation, or the functions of constituents like Noun Phrases as subject or object in a clause. All these details provide valuable information for advanced content analytics of unstructured text.

Linguistic analyses like constituent structures provide a valuable information source for semantic relations between units in sentences, as well as in text. Understanding syntactic structures and the information encoded in NLP outputs like constituent trees is valuable in many advanced applications of Natural Language Understanding and Artificial Intelligence.

Contect

Personal website: Damir Cavar